16

I have a problem with 6 classes. So I build a multiclass classifier, as follows: for each class, I have one Logistic Regression classifier, using One vs. All, which means that I have 6 different classifiers.

I can report a confusion matrix for each one of my classifiers. But, I would like to report a confusion matrix for ALL the classifiers, as I've seen in a lot of examples here.

How can I do it? Do I have to change my classification strategy, using a One vs. One algorithm instead of One vs. All? Because on these confusion matrices, the reports says the false positives for each class.

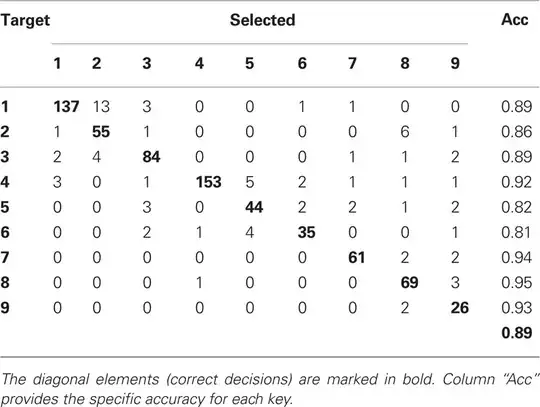
Example of a multiclass confusion matrix

Multiclass Confusion Matrix

I would like to find the number of misclassified items. In the first row, there are 137 examples of class 1 that were classified as class 1, and 13 examples of class 1 that were classified as class 2. How to get this number?

Victor Leal
  • 313
  • 1
  • 2
  • 8
  • The number of misclassified items is the sum of all elements in the matrix minus the trace of the matrix...but I don't think this is what you mean. –  Nov 02 '15 at 19:23
  • 1
    Mechanically, you get this matrix by first separating your test set by their actual class (say, Target =1, Target = 2 etc), then apply your trained classifier to each point in each group. So, for Target = 1, you would be filling in the top row of the matrix, based on how many members of this group were assigned to each class. –  Nov 02 '15 at 19:24
  • This is exactly the way it should be done.... So mechanical as you said. Thanks! – Victor Leal Nov 10 '15 at 12:51
  • 1
    no problem. I mentioned this more formally in my post as well, but sometimes it helps to see the actual recipe. –  Nov 10 '15 at 19:49

3 Answers3

15

While there are some answers already on this forum I thought I'd give the explicit equations to make it more definite:

Assuming you have a multi-class confusion matrix of the form, \begin{align} C=\text{Actual}\begin{matrix} & \text{Classifed} & \\ c_{11} & ... & c_{1n}\\ \vdots & \ddots & \\ c_{n1} & & c_{nn} \end{matrix} \end{align}

The confusion elements for each class are given by:

$tp_i = c_{ii}$

$fp_i = \sum_{l=1}^n c_{li} - tp_i$

$fn_i = \sum_{l=1}^n c_{il} - tp_i$

$tn_i = \sum_{l=1}^n \sum_{k=1}^n c_{lk} - tp_i - fp_i - fn_i$

Koen Tiels
  • 3
  • 3
Josh Albert
  • 253
  • 2
  • 5
5

Presumably, you are using these classifiers to help choose one particular class for a given set of feature values (as you said you are creating a multiclass classifier).

So, lets say you have $N$ classes, then your confusion matrix would be an $N\times N$ matrix, with the left axis showing the true class (as known in the test set) and the top axis showing the class assigned to an item with that true class. Each element $i,j$ of the matrix would be the number of items with true class $i$ that were classified as being in class $j$.

This is just a straightforward extension of the 2-class confusion matrix.

  • Yes! I know about that! But, how to say the false positives? I mean, there are examples where the number of items misclassified are shown....and my classifiers just say "Hey, there are 60 items of class A, and 40 are of another class (I just can't say which one it is...)" – Victor Leal Nov 02 '15 at 18:10
  • 1
    @VictorLeal I don't follow, a confusion matrix will tell you false positive, true positive, true negatives, false negatives..what is missing? –  Nov 02 '15 at 18:46
  • 1
    @VictorLeal see here: https://en.wikipedia.org/wiki/Confusion_matrix –  Nov 02 '15 at 18:47
  • I know the information that we have in a Confusion Matrix. Maybe an image can represents better what I'm talking about: [Confusion Matrix Multiclass](http://www.frontiersin.org/files/Articles/10335/fnins-05-00099-r4/image_m/fnins-05-00099-t003.jpg) – Victor Leal Nov 02 '15 at 18:57
  • @VictorLeal It looks like a normal confusion matrix to me...LHS shows the actual class the the top shows the assigned class...am I missing something? Also, you should add this image to your post..it will be helpful –  Nov 02 '15 at 18:59
  • The diagonal shows me the True Positives, but see that in the first line there are a number for the items that were of class 1 but were classified as being of class 2..... how to find this number? This is what I'm looking for.... – Victor Leal Nov 02 '15 at 19:00
  • I detailed it on the post – Victor Leal Nov 02 '15 at 19:04
  • @VictorLeal - well, how did you find the on-diagonal numbers? This matrix is generated from a test set, so you should know which class each test point belongs to. –  Nov 02 '15 at 19:21
  • Great explanation. So, how we can plot roc curve for multiclass? – Ali Ahmed Apr 22 '18 at 11:17
  • @VictorLeal In the end, you should have one and only one final class assignment for each sample. Your Class A classifier will call some samples Class A, and some samples Not Class A, while your class B classifier will call some samples Class B and others Not Class B. Every sample should belong to exactly one class, which is all you need for the confusion matrix. If you get one sample being called as belonging to multiple classes, or not belonging to any class, you don't really have a multiclass classifier. – Nuclear Hoagie Feb 06 '20 at 18:43
3

Using the matrix attached in the question and considering the values in the vertical axis as the actual class, and the values in the horizontal axis the prediction. Then for the Class 1:

  • True Positive = 137 -> samples of class 1, classified as class 1
  • False Positive = 6 -> (1+2+3) samples of classes 2, 3 and 4, but classified as class 1
  • False Negative = 18 -> (13+3+1+1) samples of class 1, but classified as classes 2, 3, 6 and 7
  • Ture Negative = 581 -> (55+1+6...+2+26) The sum of all the values in the matrix except those in column 1 and row 1
Ignacio Alorre
  • 197
  • 10