4

In general, is there an easier way of showing that a function is a copula than showing that:

  1. $C(u_1,\dots,u_d) =P(U_1\le u_1,\dots,U_d \le u_d) \quad$is nondecreasing in each $u_i \in [0,1] $

  2. $C(1,\dots,1,u_i,1,\dots,1)=u_i$

  3. $C$ is such that $P(a_1 \le U_1 \le b_1, \dots ,a_d \le U_d \le b_d) \ge 0$ for all $a_i,b_i \in [0,1]$

For example, I have a question asking me to prove that: $M(u_1,u_2)=\min \{u_1,u_2\}$ is a copula. I'm not really sure how I'd show the 3rd condition holds, while the first 2 follow immediately from the properties of the minimum.

WeakLearner
  • 1,013
  • 1
  • 12
  • 23
  • (3) doesn't state anything. Did you leave something out? – whuber Nov 01 '15 at 16:16
  • @whuber , yes, should say $\ge 0 $ – WeakLearner Nov 02 '15 at 05:29
  • 1
    The most straightforward way is to divide it into cases. There are six possibilities for the ordering of $(a_1,a_2,b_1,b_2)$, falling into two symmetric groups (depending on the ordering of $b_1$ and $b_2$), so you only have three easy cases to check. BTW, you also have to show that $C$ reduces to $0$ whenever at least one of its arguments if $0$. – whuber Nov 02 '15 at 16:16

1 Answers1

4

Sometimes an easy way to show that a function of $n$ real variables is a copula is to exhibit it as the (cumulative) probability function of a particular random variable with uniform marginal distributions on the unit cube $[0,1]^n$. This thought leads immediately (and uniquely) to the following demonstration.

Let $(X,Y)$ be a bivariate random variable having a uniform distribution along the line segment $I$ from $(0,0)$ to $(1,1)$. By definition, this means that the probability that $(X,Y)$ is in some rectangle $B=[x_1,x_2]\times [y_1,y_2]$ is proportional to the length of $I$ lying inside $B$. It is geometrically obvious that

$$\Pr((X,Y)\in [0,x]\times [0,y]) = \min(x,y).$$

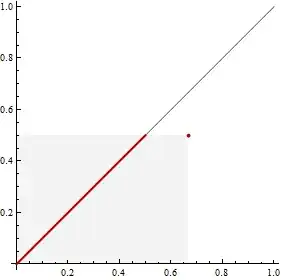
enter image description here

The dot shows a point $(x,y)$. The intersection of $I$ (shown as a gray diagonal line) with the rectangle $[0,x]\times [0,y]$ (shown as a shaded rectangle) is the thick red line. Its length is proportional to the smaller of $x$ and $y$; that is, to $\min(x,y)$.

The chance that $(X,Y)$ lies in an arbitrary rectangle $[x_1,x_2]\times [y_1,y_2] \subset [0,1]\times [0,1]$ is given by the inclusion-exclusion principle as

$$\eqalign{ \Pr((X,Y) \in [x_1,x_2]\times [y_1,y_2]) &= \Pr((X,Y)\in [0,x_2]\times[0,y_2]) - \Pr((X,Y)\in [0,x_1]\times[0,y_2]) - \Pr((X,Y)\in [0,x_2]\times[0,y_1]) + \Pr((X,Y)\in [0,x_1]\times[0,y_1]) \\ &= \min(x_2,y_2) - \min(x_1,y_2) - \min(x_2, y_1) + \min(x_1,y_1). }$$

The left hand side, because it is a probability, is non-negative, proving (3).

Incidentally, in addition to (2), you also have to show that $M(u,v) = 0$ whenever one of $u,v$ is $0$ (and all the others are in $[0,1]$)--but that's obvious. You do not have to demonstrate (1): it's a consequence of the other properties.

This demonstration extends without any essential modification to the $n$-dimensional copula $M(u_1,u_2,\ldots,u_n) = \min(u_i)$.

whuber
  • 281,159
  • 54
  • 637
  • 1,101