My MCMC do not overlap : Mixturemodel with JAGS and R

Question

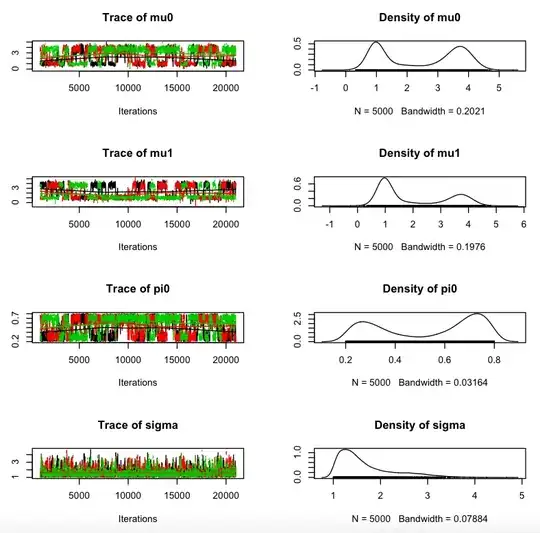
I fitted a JAGS model and I have those results :

My questions are: Why do my chains not overlap, and how can I fix that?

I used the following method:

My model is a mixture Gaussian model of two population with the same unknown variance $\sigma$. The proportion of the two population is $\pi_0$ also unknown and the mean of the two responses are obviously unknown: $\mu_0$ (associate with the proportion $\pi_0$) and $\mu_1$.

Mathematical model:

Let $ n \in \mathbb{N} $ , $\pi_0 \in \; ]0,1[ \,$ and $(\mu_0,\mu_1,\sigma) \in \mathbb R^2\times\mathbb R^+$.

I define the following function $\mu : x \in (0,1) \rightarrow (1-x)\times\mu_0 + x\times\mu_1 $

$(X_i)_{i \in [1,n]}$ and $(Z_i)_{i \in [1,n]}$ are two family of random variable defined by: $$ Z_i \tilde\ Bernoulli(\pi_0) \quad \& \quad X_i|Z_i\tilde\ \mathcal{N}(mu(Z_i),\sigma) $$

Data:

I generate a dataset following the mathematical model above:

n   = 100 # number of points
pi0 = 1/4 # proportion of points in the class 1
pi1 = 1-pi0 # proportion of points in the class 2
mu0 = 1 # mean of the class 1
mu1 = 4 # mean of the class 2
sd0 = 1 # sd of the class 1
sd1 = 1 # sd of the class 2
Z = rbinom( n , size=1 , prob=pi0 ) # Hidden information
X = rep( 0 , n ) # Information
X[Z==1] = rnorm(sum(Z) , mean=mu1 , sd=sd1 )
X[Z==0] = rnorm(n-sum(Z) , mean=mu0 , sd=sd0 )
plot(X,rep(0,n),col=Z*2+2,pch=0)

Now with the only information in my vector X, I want to find my four parameters ($\pi_0$, $\mu_0$, $\mu_1$ and $\sigma$). To do that I used JAGS to compute a mixture model.

NB: I also used the package Mclust but I want to code my own model to be able to complexity it later.

R Code

I built the following jags model:

top = 2*qnorm(0.925,mean=mean(X),sd=1.5*sd(X))
bot = 2*qnorm(0.025,mean=mean(X),sd=1.5*sd(X))

write(
paste(
 'model
 {
  for(i in 1:',n,')
  {
   Z[i] ~ dbern(pi0)
   mu[i] <- Z[i]*mu1 + (1-Z[i])*mu0
   X[i] ~ dnorm(mu[i],1/sigma)
  }
  sigma ~ dunif(1,5)
  mu1 ~ dunif(',bot,',',top,')
  mu0 ~ dunif(',bot,',',top,')
  pi0 ~ dunif(0.2,0.8)
 }'
,sep=""), "basic_mixture.txt")

And I computed the model:

# Compilation of the model
d <- list(X=X)
jm <- jags.model("basic_mixture.txt",data=d,n.chains=3)

# Chain generation 
thin = 4
jmc <- coda.samples(jm,c("pi0","mu1","mu0","sigma"), n.iter=5000*thin, 
                    thin=thin)
plot(jm)

The result of the last plot creates the first graphical.

I haven't a great experience in MCMC and JAGS code so my problem can be probably obviously solved but if you have some references that can help me to have a better understanding of the problem I'm very interested too.

Answer 1

Imagine you have a mixture of two normal distributions, the one on the left (L) and the one on the right (R) side of the plot presented below. To estimate $\mu_L$ and $\mu_R$ parameters you decide to use MCMC approach. Generally, in such case you would draw lots of random values so to substitute the $\mu_L$ and $\mu_R$ parameters and among those values you would look for the best candidates. The problem is that the sampler is dumb, it does not know that "obviously" $\mu_L$ < $\mu_R$, so sometimes it produces such values where $\mu_L$ < $\mu_R$ and sometimes the opposite. This is called the label switching problem and it is very common problem when estimating mixtures with MCMC. It is called label switching because what you get from such simulation is two vectors $\boldsymbol{\mu_1}$ and $\boldsymbol{\mu_2}$ and each of those vectors would contain samples for both $\mu_L$ and $\mu_R$ parameters, sampler would not "know" that it should save all $\mu_L$ in $\boldsymbol{\mu_1}$ and $\mu_R$ in $\boldsymbol{\mu_2}$, so from time to time (randomly!) it would switch.

What could be done about this problem? In such simple case there is an obvious solution: force an restraint that always $\mu_L$ < $\mu_R$ (e.g. having two values simply sort them before assignment to mu1 and mu2 variables, or using different informative priors for each value). There is more ways of dealing with this problem (see this thread), but unfortunately they not always work and not always are so simple as the one described.

In many cases the problem is pretty easy to spot on traceplots. For example, look at the traceplots that you provided. If you compare plots for mu0 and mu1, you will notice that until 3000th iteration the green chain was sampling for the "higher" $\mu$ and then switched to "lower" $\mu$, to make many more such exchanges during the whole simulation.