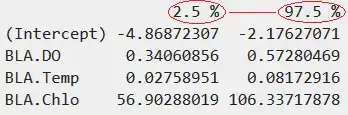
I am new to using R and its bit hard for me to understand the output. I have here the glm ouptput and I am basically looking for confidence interval. Is my output (confint(fitBLA17)) showing a 97.5% confidence interval?
fitBLA16 <- glm(BLA.DOC~BLA.DO + BLA.Temp+BLA.Chlo,data=swan, family=gaussian(link=log))
> summary(fitBLA16)
Call:
glm(formula = BLA.DOC ~ BLA.DO + BLA.Temp + BLA.Chlo, family = gaussian(link = log),
data = swan)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.26276 -0.42484 -0.07066 0.30826 2.01178
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.51962 0.68938 -5.105 4.10e-06 ***
BLA.DO 0.45738 0.05926 7.719 2.25e-10 ***
BLA.Temp 0.05454 0.01398 3.903 0.000258 ***
BLA.Chlo 81.67750 12.55730 6.504 2.27e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for gaussian family taken to be 0.4415451)
Null deviance: 150.516 on 59 degrees of freedom
Residual deviance: 24.726 on 56 degrees of freedom
AIC: 127.08
Number of Fisher Scoring iterations: 4
> confint(fitBLA16)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) -4.86872307 -2.17627071
BLA.DO 0.34060856 0.57280469
BLA.Temp 0.02758951 0.08172916
BLA.Chlo 56.90288019 106.33717878