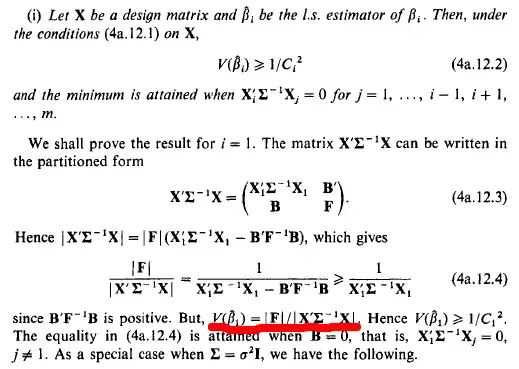How is the determinant of $(X'X)$ related to variance?

Question

I'm working on a problem (and actually have the answer) but I don't know why this is the answer, can someone explain this equality?. It has to do with the the determinant of the partitioned matrix $(X'X).$

Let $$X=[x_0, x_1, \ldots,x_{k-1},x_k]=[W,x_k] $$ and let $\operatorname{rank}(X)=k+1$

a.) show that $|X'X|=|W'W|(x_k'x_k-x_k'W(W'W)^{-1}W'x_k)$

which is fairly obvious by the partitioned matrix

$$(X'X)=(W,x_k)'(W,x_k)$$ which has a determinant equal to $$|W'W|(x_k'x_k-x_k'W(W'W)^{-1}W'x_k)$$

b though is harder.

b.) from a, deduce $|W'W|/|X'X|>1/x_k'x_k$, use this to show that in the usual linear model $y=X\beta + \epsilon, \operatorname{Var}(\widehat{\beta}_k)\geq\sigma^2(x_k,x_k)$

With the information below, I am able to solve this problem, but why does the equality below hold?

the part i have underlined was just a given and I'm not sure what the deal is with it, could anyone explain to me how determinant and variance are connected like this?

Answer 1

This is a result of using Cramer's rule to calculate the inverse of $\mathbf{X}^{\prime}\Sigma^{-1}\mathbf{X}$.

Note that the matrix $(\mathbf{X}^{\prime}\Sigma^{-1}\mathbf{X})^{-1}$ is the covariance matrix of the parameters $\beta_i$. So $$ \text{Var}(\beta_1) = (\mathbf{X}^{\prime}\Sigma^{-1}\mathbf{X})^{-1}_{1,1} $$ The first element in the matrix above is the variance of this parameter $\beta_1$. Now to calculate this value we can use Cramer's rule. To use Cramer's rule to find the inverse of a matrix $A$ we have $$ A^{-1} = \frac{1}{\text{det}(A)}\text{Adj}(A) $$ In this case $A=\mathbf{X}^{\prime}\Sigma^{-1}\mathbf{X}$, and the element we are seeking in $\text{Adj}(A)$ is $|F|$.

Cramer's rule is a very ineffective way of computing an inverse compared to standard methods. This rule usually pops up in situations like these, where one needs an expression for a specific element in the inverse.