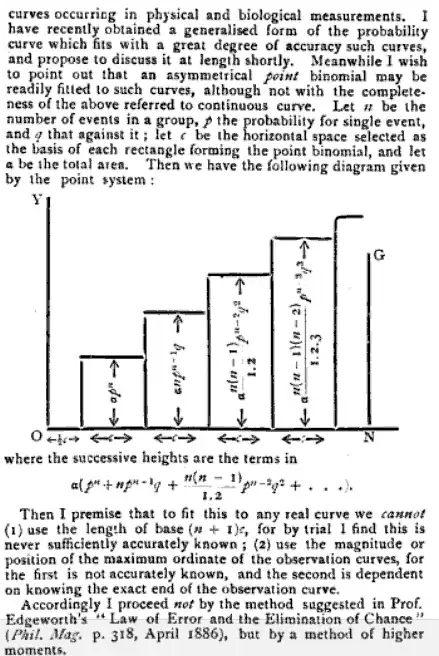
Question: So what does the word "moment" mean in this case? Why this choice of word? It doesn't sound intuitive to me (or I never heard it that way back in college :) Come to think of it I am equally curious with its usage in "moment of inertia" ;) but let's not focus on that for now.
Answer: Actually, in a historical sense, moment of inertia is probably where the sense of the word moments comes from. Indeed, one can (as below) show how the moment of inertia relates to variance. This also yields a physical interpretation of higher moments.
In physics, a moment is an expression involving the product of a distance and a physical quantity, and in this way it accounts for how the physical quantity is located or arranged. Moments are usually defined with respect to a fixed reference point; they deal with physical quantities as measured at some distance from that reference point. For example, the moment of force acting on an object, often called torque, is the product of the force and the distance from a reference point, as in the example below.
Less confusing than the names usually given, e.g., hyperflatness etc. for higher moments would be moments from circular motion e.g., moments of inertia for circular motion, of rigid bodies which is an simple conversion. Angular acceleration is the derivative of angular velocity, which is the derivative of angle with respect to time, i.e., $ \dfrac{d\omega}{dt}=\alpha,\,\dfrac{d\theta}{dt}=\omega$. Consider that the second moment is analogous to torque applied to a circular motion, or if you will an acceleration/deceleration (also second derivative) of that circular (i.e., angular, $\theta$) motion. Similarly, the third moment would be a rate of change of torque, and so on and so forth for yet higher moments to make rates of change of rates of change of rates of change, i.e., sequential derivatives of circular motion. This is perhaps easier to visualize this with actual examples.
There are limits to physical plausibility, e.g., where an object begins and ends, i.e., its support, which renders the comparison more or less realistic. Let us take the example of a beta distribution, which has (finite) support on [0,1] and show the correspondence for that. The beta distribution density function (pdf) is
$$\beta(x;\alpha,\beta)=\begin{array}{cc}
\Bigg\{ &
\begin{array}{cc}
\dfrac{x^{\alpha -1} (1-x)^{\beta -1}}{B(\alpha ,\beta )} & 0<x<1 \\
0 & \text{True} \\
\end{array}
\\
\end{array}\,,$$
where $B(\alpha,\beta)=\dfrac{\Gamma(\alpha)\,\Gamma(\beta)}{\Gamma(\alpha+\beta)}$, and $\Gamma(.)$ is the gamma function, $\Gamma(z) = \int_0^\infty x^{z-1} e^{-x}\,dx$.
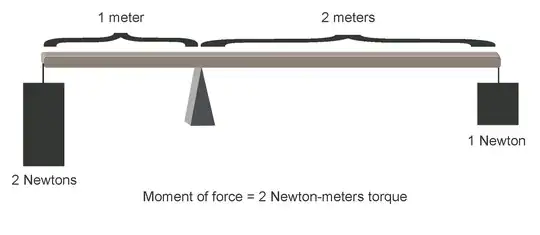
The mean is then the first moment of rotation around the $z$-axis for the beta function plotted as a rigidly rotating thin sheet of uniform area density with the minimum $x$-value affixed to the (0,0,0) origin, with its base in the $x,y$ plane.
$$\mu=\int_0^1r\,\beta(r;\alpha,\beta)\,dr=\frac{\alpha}{\alpha+\beta}\,,$$
as illustrated for $\beta(r;2,2)$, i.e., $\mu=\dfrac{1}{2}$, below
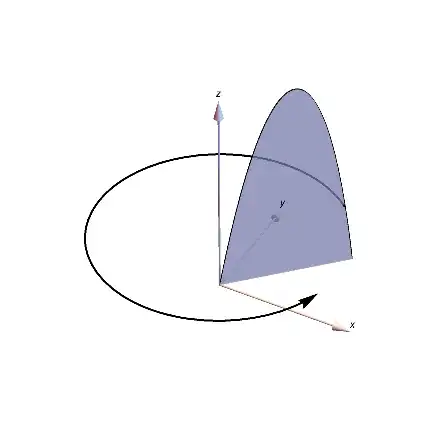
Note that there is nothing preventing us from moving the beta distribution thin sheet to another location and re-scaling it, e.g., from $0\leq r\leq1$ to $2\leq r\leq4$, or changing the vertical shape, for example to be a paddle rather than a hump.
To calculate the beta distribution variance, we would calculate the moment of inertia for a shifted beta distribution with the $r$-value mean placed on the $z$-axis of rotation,
$$\sigma^2=\int_0^1 (r-\mu)^2 \beta(r;\alpha,\beta) \, dr =\frac{\alpha \beta }{(\alpha +\beta )^2 (\alpha +\beta +1)}\,,$$
which for $\beta(r;2,2)$, i.e., $I=\sigma^2=\dfrac{1}{20}$, where $I$ is the moment of inertia, looks like this,
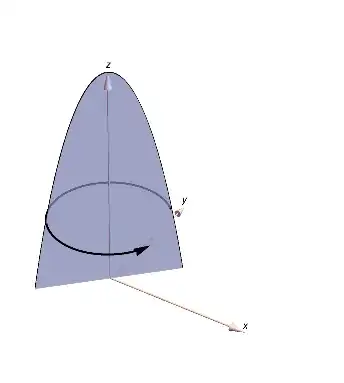
Now for higher so called 'central' moments, i.e., moments about the mean, like skewness, and kurtosis we calculate the $n^{\text{th}}$ moment around the mean from
$$\int_0^1 (r-\mu)^n \beta(r;\alpha,\beta) \, dr\,.$$
This can also be understood to be the $n^{\text{th}}$ derivative of circular motion.
What if we want to calculate backwards, that is, take a 3D solid object and turn it into a probability function? Things then get a bit trickier. For example, let us take a torus.
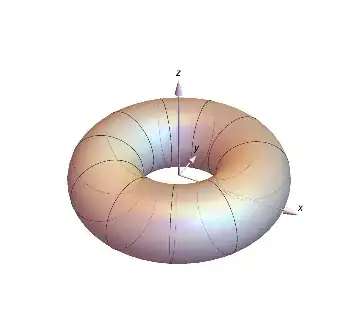
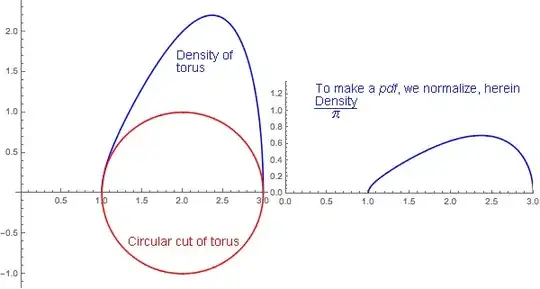
First we take its circular cross section, then we make it into a half ellipse to show the density of any flat coin like slice, then we convert the coin into a wedge-shaped coin to account for the increasing density with increasing distance ($r$) from the $z$-axis, and finally we normalize for the area to make a density function. This is outlined graphically below with the mathematics left to the reader.
Finally, we ask how these equivalences relate to motion? Note that as above the moment of inertia, $I$, can be made related to the second central moment, $\sigma^2$, A.K.A., the variance. Then $I=\dfrac{\tau}{a}$, that is, the ratio of the torque, $\tau$, and the angular acceleration, $a$. We would then differentiate to obtain higher order rates of change in time.