2

I have a data matrix $X$ and I perform a PCA on this data with:

%// Subtract the mean from the data
Y = bsxfun(@minus, X, mean(X));

%// Obtain the PCA solution by calculate the SVD of Y
[U, S, V] = svd(Y);

%// Compute variance explained
rho = diag(S).^2./sum(diag(S).^2);

%// Plot variance explained
plot(rho, 'o-')
title('Variance explained by principal components');
xlabel('Principal component');
ylabel('Variance explained');

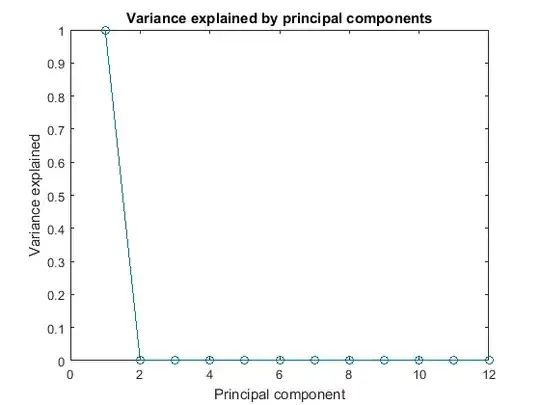
I get this plot

enter image description here

What is the reason for this to happen? It cannot be correct that only the first PC can explain all the variance.

My data looks like

price       crime      nox        rooms      dist          radial  proptax    stratio   lowstat   lprice     lnox      lproptax
==========================================================================================================================
24000       .006       5.38       6.57       4.09          1       29.6       15.3       4.98   10.08581   1.682688    5.69036  
21599       .027       4.69       6.42       4.97          2       24.2       17.8       9.14   9.980402   1.545433   5.488938  
34700       .027       4.69       7.18       4.97          2       24.2       17.8       4.03    10.4545   1.545433   5.488938  
33400       .032       4.58          7       6.06          3       22.2       18.7       2.94   10.41631   1.521699   5.402678  
...

so the values of first attribute are much higher than the rest. Can this be the reason to the weird "variance explained" plot?

amoeba
  • 93,463
  • 28
  • 275
  • 317
Jamgreen
  • 363
  • 1
  • 3
  • 9
  • 3
    Yes. The "total variance" of your dataset is simply the sum of the variances of all the variables. Your `price` variable will dominate the sum, and hence the PC1 will essentially equal to `price` and will explain almost all the variance. You probably want to run PCA on correlations not on covariances (see http://stats.stackexchange.com/questions/53), i.e. you probably should standardize your data after centering but prior to doing SVD: `Y = bsxfun(@times, Y, 1./std(Y));` – amoeba Sep 28 '15 at 16:52
  • But I thought I was standardizing with `Y = bsxfun(@minus, X, mean(X));`? – Jamgreen Sep 28 '15 at 16:54
  • 2
    No, that's just centering. The variances can still be very different, check for yourself by running `var(Y)`. – amoeba Sep 28 '15 at 16:55
  • Ah ok. Thanks! But you say that `price` will dominate the sum, and hence the PC1 will be equal to `price`.. As I have understood I cannot say that PC1 is related to any of the variables. Am I right? – Jamgreen Sep 28 '15 at 16:58
  • 1
    PC1 is just a linear combination of your original variables. Of course you can see how they are related. If you don't standardize, it will be $\sim1$ times `price` plus $\sim 0$ times everything else. – amoeba Sep 28 '15 at 17:00
  • 2
    See http://stats.stackexchange.com/questions/87037/which-variables-explain-which-pca-components-and-vice-versa for another example in which uncritical use of covariance matrix produced garbage, which was not even noticed by all contributors to the thread. – Nick Cox Sep 28 '15 at 17:11
  • 1
    After some reflection, I edited the top answer in the "PCA on correlation or covariance" thread (to include some plots) and I think this question is now a duplicate of that one. In the dataset considered there PCA on covariance explains over 98% of the variance. – amoeba Sep 29 '15 at 11:31

0 Answers0