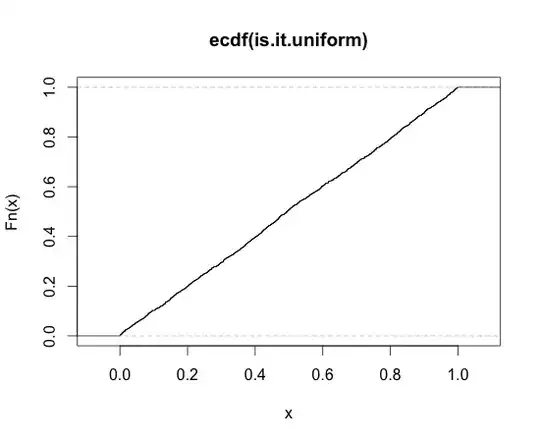
Here is the simulation confirming @Simon Byrne's answer:
#demonstrate a'S a is inverse gamma when S is inverse Wishart W^-1(n,Sg^-1),
#for vector a, with scale a'Sg^-1 a / 2...
rwish <- function(n,Sg) {
#generate variates from W(n,Sg) wishart distribution, the slow way
#rwishart from bayesm library is probably faster
C <- chol(Sg)
p <- dim(Sg)[1]
X <- matrix(rnorm(n*p),nrow=n) %*% C
Z <- t(X) %*% X
}
rinvwishprod <- function(n,a,Sg=diag(x=1,nrow=length(a),ncol=length(a))) {
#a' X a, where X is inv-wishart with parameters n and Sg^-1
X <- rwish(n,Sg)
t(a) %*% solve(X,a)
}
set.seed(1729)
n <- 256
p <- 16
ntrial <- 2048
#generate a PSD matrix Sg
X <- matrix(rnorm(2*p*p),nrow=2*p,ncol=p)
Sg <- t(X) %*% X
#generate vector a
a <- matrix(rnorm(p),nrow=p)
#draw many variates from this process
many.rv <- replicate(ntrial,rinvwishprod(n,a,Sg))
#try to transform to uniform RV using the inverse gamma law
alpha <- (n - p + 1) / 2
beta <- (t(a) %*% solve(Sg,a)) / 2
is.it.uniform <- pgamma(1 / many.rv,shape=alpha,rate=beta)
#plot the results
plot(ecdf(is.it.uniform))
Basically I generate, for fixed $\Sigma, n, \vec{a}$, variates of the form $v = \vec{a}^{\top}S^{-1}\vec{a}$, where $S \sim \mbox{W}\left(n,\Sigma\right)$, then compute the CDF under the inverse gamma relationship (shape parameter $\alpha = (n - p + 1)/2$ and scale parameter $\beta = \vec{a}^{\top}\Sigma^{-1}\vec{a}/2$). The resultant 'p-value' should be uniform, which is confirmed visually: