2

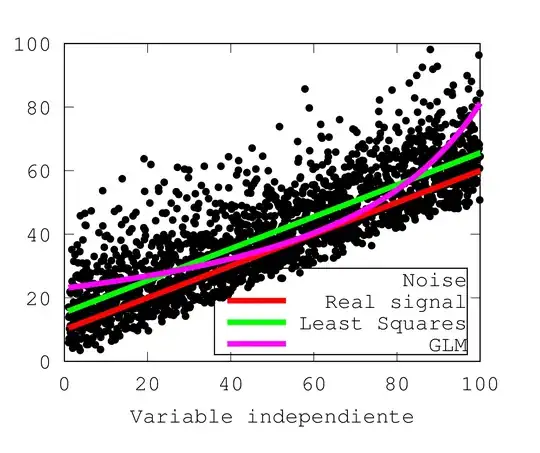
To illustrate the usefulness of GLMs in comparison to the least square method I did a simple program in which I add random noise to a straight line (Y=m*x + b; red line in the attached plot). The noise is coming from a Gamma distribution "centered" on zero (the mode, i.e., the maximum of the gamma distribution is lying over zero). When I plot this artificial signal (Y + g_noise; black dots in the plot) together with Y, I see Y nicely cutting the noise dots in the region of maximum density. I though this simple model of a straight line and asymmetrical not-normal noise is an "easy" task for a GLM and should exemplify its superior performance in comparison to least squares. So, I take Y as input of 2 linear models:

  1. The classical least squares (Y_ls; green line in the plot). As expected, Y_ls is unable of reproducing the original signal Y but it performs quite good: It makes a straight line parallel to Y, cutting the noise dots not in the region of maximum density but in the "middle". Namely, Y_ls has offset in comparison to Y. This is in agreement with the Gauss-Markov theorem, since the noise is not normal, least squares cannot yield an unbiased linear estimator. I was expected this, so far so good.

  2. A GLM with a Gamma canonical link. To my big surprise, Y_glm (magenta curve) is not only unable of reproducing the original signal, but from my point of view it even performs worse than Y_ls: It only fits the original signal in the middle of the distribution, which is OK, but at the beginning and end of the record Y_glm is a considerable poorer estimation in comparison to Y_ls, to the naked eye. A GLM with an identity link but Gamma variance ($\mu^2$) should, from my point of view, also performs well, but it simply reproduces Y_ls, meaning no improvement over least squares.

So, my questions are:

  1. Am I misunderstanding the sense of a GLM? Am I doing something wrong? Is this really the best we can get of a GLM in comparison to least squares?

  2. Is there another model (perhaps a GAM?) which would really be able of seeing through the data, identifying the Gamma noise and correctly reproducing the original line Y (the red line)?enter image description here

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
nukimov
  • 562
  • 3
  • 13

1 Answers1

5

Your main problem is that the link is a non-linear transformation. The default (canonical) link function for the Gamma distribution is the reciprocal (the log is also common). You should do better with a Gamma response but an identity link, given the way you generated the data.

In addition, all these models are for the mean of your conditional distribution. It seems you centered your data using the mode. That's why the linear model is shifted vertically relative to the red line.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • 2
    The answer given is perfect, I would just want to add (many years now after I asked myself this question and am a bit smarter about GLMs), that the example I chose is unable of exemplifying the advantages of a GLM over the simple LS model, since the data was generated in a homoscedastically. – nukimov Dec 04 '20 at 08:32
  • @nukimov, if you want to know how to generate data to illustrate the advangages of a gamma GLM over OLS, you could ask a new question. It's quite doable. – gung - Reinstate Monica Dec 04 '20 at 12:32