Clustering -- Intuition behind Kleinberg's Impossibility Theorem

Question

I've been thinking about writing a blog post on this interesting analysis by Kleinberg (2002) that explores the difficulty of clustering. Kleinberg outlines three seemingly intuitive desiderata for a clustering function and then proves that no such function exists. There are many clustering algorithms that satify two of the three criteria; however, no function can satisfy all three simultaneously.

Briefly and informally, the three desiderata he outlines are:

• Scale-Invariance: If we transform the data so that everything is stretched out equally in all directions, then the clustering result shouldn’t change.
• Consistency: If we stretch the data so that the distances between clusters increase and/or the distances within clusters decrease, then the clustering result shouldn’t change.
• Richness: The clustering function should theoretically be able to produce any arbitrary partition/clustering of datapoints (in the absence of knowing the pairwise distance between any two points)

Questions:

(1) Is there a good intuition, geometric picture that can show the inconsistency between these three criteria?

(2) This refers to technical details to the paper. You will have to read the link above to understand this portion of the question.

In the paper, the proof to theorem 3.1 is a bit hard for me to follow at points. I'm stuck at: "Let $f$ be a clustering function that satisfies Consistency. We claim that for any partition $\Gamma \in \text{Range}(f)$, there exist positive real numbers $a < b$ such that the pair $(a, b)$ is $\Gamma$-forcing."

I don't see how this can be the case... Isn't the partition below a counter-example where $a > b$ (i.e. minimum distance between clusters is greater than maximum distance within clusters)?

Edit: this is clearly not a counterexample, I was confusing myself (see answers).

---

Other papers:

• Ackerman & Ben-David (2009). Measures of Clustering Quality: A Working Set of Axioms for Clustering
  • Points out some issues with the "consistency" axiom

Answer 1

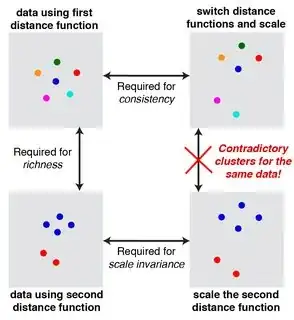
One way or another, every clustering algorithm relies on some notion of “proximity” of points. It seems intuitively clear that you can either use a relative (scale-invariant) notion or an absolute (consistent) notion of proximity, but not both.

I will first try to illustrate this with an example, and then go on to say how this intuition fits with Kleinberg’s Theorem.

An illustrative example

Suppose we have two sets $S_1$ and $S_2$ of $270$ points each, arranged in the plane like this:

$\hskip{6em}$

You might not see $270$ points in either of these pictures, but that’s just because many of the points are very close together. We see more points when we zoom in:

$\hskip{3em}$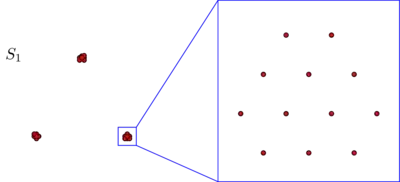

You’ll probably spontaneoulsy agree that, in both data sets, the points are arranged in three clusters. However, it turns out that if you zoom in on any of the three clusters of $S_2$, you see the following:

$\hskip{3em}$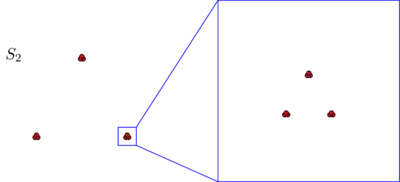

If you believe in an absolute notion of proximity, or in consistency, you’ll still maintain that, irrespective of what you just saw under the microscope, $S_2$ consists of just three clusters. Indeed, the only difference between $S_1$ and $S_2$ is that, within each cluster, some points are now closer together. If, on the other hand, you believe in a relative notion of proximity, or in scale invariance, you’ll feel inclined to argue that $S_2$ consists not of $3$ but of $3×3 = 9$ clusters. Neither of these points of view is wrong, but you do have to make a choice one way or the other.

A case for isometry invariance

If you compare the above intuition with Kleinberg’s Theorem, you will find that they are slightly at odds. Indeed, Kleinberg’s Theorem appears to say that you can achieve scale invariance and consistency simultaneously as long as you do not care about a third property called richness. However, richness is not the only property you lose if you simultaneously insist on scale invariance and consistency. You also lose another, more fundamental property: isometry-invariance. This is a property that I wouldn’t be willing to sacrifice. As it doesn’t appear in Kleinberg’s paper, I’ll dwell on it for a moment.

In short, a clustering algorithm is isometry invariant if its output depends only on the distances between points, and not on some additional information like labels that you attach to your points, or on an ordering that you impose on your points. I hope this sounds like a very mild and very natural condition. All algorithms discussed in Kleinberg’s paper are isometry invariant, except for the single linkage algorithm with the $k$-cluster stopping condition. According to Kleinberg’s description, this algorithm uses a lexicographical ordering of the points, so its output may indeed depend on how you label them. For instance, for a set of three equidistant points, the output of the single linkage algorithm with the $2$-cluster stopping condition will give different answers according to whether you label your three points as “cat”, “dog”, “mouse” (c < d < m) or as “Tom”, “Spike”, “Jerry” (J < S < T):

$\hskip{6em}$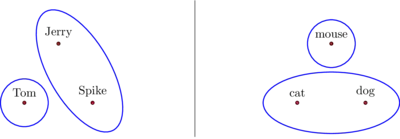

This unnatural behaviour can of course easily be repaired by replacing the $k$-cluster stopping condition with a “$(≤ k)$-cluster stopping condition”. The idea is simply not to break ties between equidistant points, and to stop merging clusters as soon as we have reached at most $k$ clusters. This repaired algorithm will still produce $k$ clusters most of the time, and it will be isometry invariant and scale invariant. In agreement with the intuition given above, it will however no longer be consistent.

For a precise definition of isometry invariance, recall that Kleinberg defines a clustering algorithm on a finite set $S$ as a map that assigns to each metric on $S$ a partition of $S$: $$ Γ\colon \{\text{metrics on } S\} → \{\text{partitions of } S\}\\ d ↦ Γ(d) $$ An isometry $i$ between two metrics $d$ and $d'$ on $S$ is a permutation $i\colon S → S$ such that $d'(i(x),i(y)) = d(x,y)$ for all points $x$ and $y$ in $S$.

Definition: A clustering algorithm $Γ$ is isometry invariant if it satisfies the following condition: for any metrics $d$ and $d'$, and any isometry $i$ between them, the points $i(x)$ and $i(y)$ lie in the same cluster of $Γ(d')$ if and only if the original points $x$ and $y$ lie in the same cluster of $Γ(d)$.

When we think about clustering algorithms, we often identify the abstract set $S$ with a concrete set of points in the plane, or in some other ambient space, and imagine varying the metric on $S$ as moving the points of $S$ around. Indeed, this is the point of view we took in the illustrative example above. In this context, isometry invariance means that our clustering algorithm is insensitive to rotations, reflections and translations.

$\hskip{6em}$

A variant of Kleinberg’s Theorem

The intuition given above is captured by the following variant of Kleinberg’s Theorem.

Theorem: There is no non-trivial isometry-invariant clustering algorithm that is simultaneously consistent and scale-invariant.

Here, by a trivial clustering algorithm, I mean one of the following two algorithms:

1. the algorithm that assigns to every metric on $S$ the discrete partition, in which every cluster consists of a single point,

2. the algorithm that assigns to every metric on $S$ the lump partition, consisting of a single cluster.

The claim is that these silly algorithms are the only two isometry invariant algorithms that are both consistent and scale-invariant.

Proof: Let $S$ be the finite set on which our algorithm $Γ$ is supposed to operate. Let $d₁$ be the metric on $S$ in which any pair of distinct points has unit distance (i.e. $d₁(x,y) = 1$ for all $x ≠ y$ in $S$). As $Γ$ is isometry invariant, there are only two possibilities for $Γ(d₁)$: either $Γ(d₁)$ is the discrete partition, or $Γ(d₁)$ is the lump partition. Let’s first look at the case when $Γ(d₁)$ is the discrete partition. Given any metric $d$ on $S$, we can rescale it so that all pairs of points have distance $≥ 1$ under $d$. Then, by consistency, we find that $Γ(d) = Γ(d₁)$. So in this case $Γ$ is the trivial algorithm that assigns the discrete partition to every metric. Second, let’s consider the case that $Γ(d₁)$ is the lump partition. We can rescale any metric $d$ on $S$ so that all pairs of points have distance $≤ 1$, so again consistency implies that $Γ(d)=Γ(d₁)$. So $Γ$ is also trivial in this case. ∎

Of course, this proof is very close in spirit to Margareta Ackerman’s proof of Kleinberg’s original theorem, discussed in Alex Williams’s answer.

Answer 2

This is the intuition I came up with (a snippet from my blog post here).

A consequence of the richness axiom is that we can define two different distance functions, $d_1$ (top left) and $d_2$ (bottom left), that respectively put all the data points into individual clusters and into some other clustering. Then we can define a third distance function $d_3$ (top and bottom right) that simply scales $d_2$ so that the minimum distance between points in $d_3$ space is larger than the maximum distance in $d_1$ space. Then, we arrive at a contradiction, since by consistency the clustering should be the same for the $d_1 \rightarrow d_3$ transformation, but also the same for the $d_2 \rightarrow d_3$ transformation.