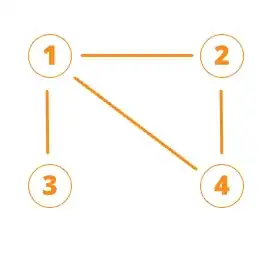
i'm studying a method to cluster similar topic represented in a graph like this:
The result must be:
[0] = 1,2,4
[1] = 3
I tried Markov Cluster Algorithm but i haven't good result.
Now i'm trying HCS cluster, but i have a doubt about Minimum cut which is only a probabilistic method.
In your experience is HCS the right algorithm to cluster a graph? A good and simple example is welcome
Thanks!