Many of the questions I've posted on SE in the last month have been in the goal of helping me solve this particular problem. The questions have all been answered, but I still can't come up with a solution. So, I figured that I should just ask the problem I'm trying to solve directly.
Let $X_n \sim F_n$, where $F_n = (1-(1-F_{n-1})^c)^c$, $F_0 = x$, $c\geq 2$ (integer), and every $F_n$ is a cdf over $(0,1)$.
I want to prove that $\mathbb{E}X_n$ decreases with $n$ for all $c$ (or even, for any particular $c$)! I can show that $F_n$ converges to a Dirac mass at the unique solution to $x_c = (1-(1-x)^c)^c)$ For $c=2$, $x_2 = (3-\sqrt{5})/2 \approx .38$. When looking at a plot of cdfs for increasing $n$'s for the same $c$, all the cdfs cross at $x_n$. The value of $F(x)$ decreases for values of $x$ less than $x_n$ and increases for values of $x$ greater then $x_n$ (as $n$ increases) converging to a vertical line at $x_n$.
Below is a plot of $\mathbb{E}X_n$ for $n = 1$ to $40$ for $c = 2$ to $7$. It is of course a discrete plot, but I have the lines joined for ease of viewing. To generate this plot, I used NIntegrate in Mathematica, though I needed to do it on $1-F^{-1}_n$, as for some reason Mathematica couldn't generate answers on high values of $n$ for the original function. The two should be equivalent, as per Young's theorem, $\int_0^1F(x)\,dx = \int_0^1 1-F^{-1}(x)\,dx$. In my case, $F^{-1}_n(x) = 1-(1-(F^{-1}_{n-1})^{\frac{1}{c}})^{\frac{1}{c}}$, $F^{-1}_n = x$.
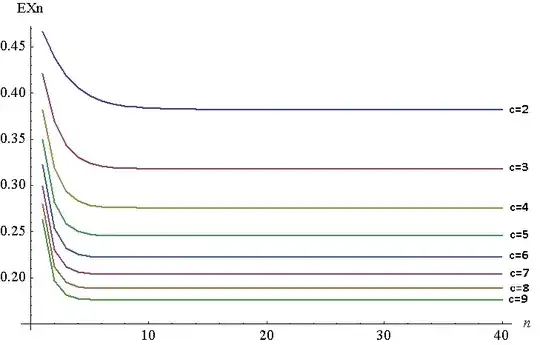
As you can see, the $EX_n$ moves very quicky to a minute distance from its fixed point $x_c$. As $c$ increases, the fixed point decreases (eventually will go to 0).
So, it certainly SEEMS to be true that $EX_n$ decreases with $n$ for all $c$. But I can't prove it. Can anyone help me out? (again, I'd be somewhat happy with even just a single $c$) And, if you can't, but you have insight as to why this particular problem may be unsolvable, please share that insight as well.