12

There are few explanations I can find that describe how to interpret linear regression coefficients after differencing a time series (to eliminate a unit root). Is it just so simple that there is no need to state it formally?

(I am aware of this question, but was not sure how general it's response was).

Lets say we are interested in the model $Y_{t}=\beta_{0}+\beta_{1}X_{1t}+\beta_{2}X_{2t} + +...+\beta_{p}X_{pt}+ \delta_{t}$ where $\delta_{t}$ is possibly ARMA(p,q). It is the $\beta_{1}$, $\beta_{2}$,...$\beta_{p}$ that are of interest. Specifically the interpretation in terms of "a 1-unit change in $X_{i}$ results in an average change in $Y_{t}$ of $\beta_{i}$" for $i = 1...p.$

Now lets say we need to difference $Y_{t}$ due to suspected non-stationarity from a unit root (e.g. ADF Test). We need to then also difference in the same manner, each of the $X_{it}$.

What is the interpretation of the $\beta_{i}$ if:

  1. The first difference $Y'_{t}$ is taken of $Y_{t}$ and each of the $X_{it}$?
  2. The second difference (difference of the difference) ($Y''_{t}$) is taken of $Y_{t}$ and each of the $X_{it}$?
  3. A seasonal difference (e.g. $(1-B^{12})$ for monthly data) is taken of $Y_{t}$ and each of the $X_{it}$?

EDIT 1

I did find one text that mentions differences and interpretation of coefficients and it sounds very similar to the linked question. This is from Alan Pankratz Forecasting with Dynamic Regression pages 119-120:

enter image description here enter image description here

Community
  • 1
B_Miner
  • 7,560
  • 20
  • 81
  • 144
  • May I assume that the time-series are monthly ? That the Y's and X's are log-transforms of economic variables ? –  Sep 05 '15 at 07:00
  • The question is more about general interpretation and if various forms of differencing, perhaps with ARMA errors, changes the interpretation from the undifferenced regression. So, no not logged :) – B_Miner Sep 05 '15 at 13:01
  • Yes but the interpretation can be as simple as $\beta_1$ is the increase in the **growth** of $y$ for a unit increase in the **growth** of $x_1$. Where 'growth' is the month-to-month growth for your question one and the 'year-to-year' growth' for you question. Growth is the absolute growth of y but if y is the log transform of $z$ then it is the relative growth of z. Is it such a kind of interpretation you are asking for ? –  Sep 05 '15 at 13:09
  • This comment adds to my confusion on the topic. I find examples where the interpretation does not change at all because the betas are unchanged after differencing, but you are implying (I think) that one needs to use the word growth which implies (I think) that the interpretation changes to the differenced data (change in Y, change in X). – B_Miner Sep 05 '15 at 13:13
  • 1
    Somewhat related answer [here](http://stats.stackexchange.com/questions/168707/coefficients-for-regression-in-levels-from-estimated-first-difference-coefficien/171157#171157). – Richard Hardy Sep 05 '15 at 15:30
  • Richard, do I read your linked question to suggest you agree with the response from f coppens below that the interpretation is unchanged? – B_Miner Sep 09 '15 at 15:03
  • Check this thread.... an econometric answer: https://stats.stackexchange.com/questions/435032/estimation-in-levels-vs-differences/435064 Interpretation is not as clear cut as implied. Only in large samples can delta b be interpreted as b. – David King Feb 05 '22 at 20:55
  • It seems that my comment has been rated negative without any explanation.... look at the numbers: the estimate of beta in levels is very, very different to that in differences. Moreover, it would appear that my hunch that these are NOT equivalent is implied by Jeff Wooldridge: Introductory Econometrics, 7th ED, pages 414-415 especially the last sentence in Example 12.7. How can betas from an equation in differences be equal (in an interpretation sense) to an equation in levels? They can't possibly be.....the original levels data has been transformed. Think about it ! – David King Feb 05 '22 at 20:39

2 Answers2

14

Let's take an example with one independent variable because that's easier in typing.

As you start from $y_t=\beta_0 + \beta_1 x_t$ then the same holds for $y_{t-1}=\beta_0 + \beta_1 x_{t-1}$.

So if I subtract the two then I get $\Delta y= \beta_1 \Delta x$. Therefore the interpretation of coefficient $\beta_1$ does not change, it is the same $\beta_1$ in each of these equations.

But the interpretation of the equation $y_t=\beta_0 + \beta_1 x_t$ is not the same as the interpretation of the equation $\Delta y= \beta_1 \Delta x$. That is what I mean.

So $\beta_1$ is the change in $y$ for a unit change in $x$ but is it also the change in the growth of $y$ for a unit change in the growth of $x$.

The reason for differencing is 'technical': if the series are non-stationary, then I can not estimate $y_t = \beta_0 + \beta_1 x_t$ with OLS. If the differenced series are stationary , then I can use the estimate of $\beta_1$ from the equation $\Delta y= \beta_1 \Delta x$ as as an estimate for $\beta_1$ in the equation $y_t=\beta_0 + \beta_1 x_t$, because it is the same $\beta_1$.

So differencing is a 'technical' trick for finding an estimate of $\beta_1$ in $y_t = \beta_0 + \beta_1 x_t$ when the series are non-stationary. The trick makes use of the fact that the same $\beta_1$ appears in the differenced equation.

Obviously this is not different if there are more than one independent variable.

Note: all this is a consequence of the linearity of the model, if $y=\alpha x + \beta$ then $\Delta y = \alpha \Delta x$ , so the $\alpha$ is at the same time the change in $y$ for a unit change in $x$ but also the change in the growth of y for a unit change in the growth of $x$, it is the same $\alpha$.

  • So the interpretation is both ways. But the main point is that if there is differencing (any type of the three in my question or combinations thereof) the original undifferenced beta is still estimated (so the original research question of interest is still available). Correct? Does that still hold if there are Arma errors? – B_Miner Sep 05 '15 at 15:23
  • Well if you estimate the $\beta_1$ from the differenced equation, then this estimated $\hat{\beta}_1$ is also an estimate for the $\beta_1$ in the undifferenced equation (because it is the same $\beta_1$). The point is that, in the equation for which you do the estimation, the series must be stationary, then all is fine (else you do not get estimators with desirable properties like unbiasedness). A drawback is of course that you can not estimate $\beta_0$ in this way, so if you want an estimate for $\beta_0$ you will have to look at co-integration. –  Sep 05 '15 at 15:40
  • An intercept is rarely of interest though it seems, more important is the B1 to BP that are the coefficients on continuous or dummy variables of interest. And just to clairify, nothing changes in this regard if the errors are not iid but we use ARMA errors? I would guess one needs to consider that in the interpretation with or without differences correct (as the "all else being equal" includes lagged (with AR) values of y being controlled for)? – B_Miner Sep 05 '15 at 15:56
  • And to round out the original question - this holds for any differencing (seasonal + first difference etc)? – B_Miner Sep 05 '15 at 15:59
  • 1
    ARMA errors do not change anything to the interpretation. The only technical matter is that, after differencing you have to have stationary series else the estimate of $\beta_1$ is biased, so if you have ARMA errors but after differencing you get stationary series, then in my opinion all is fine. –  Sep 05 '15 at 15:59
  • 1
    For seasonal differencing you also get the same $\beta_1$ in the differenced equation as in the 'original' equation, so everything remains valid. In fact, whatever you do, as long as you can show that after the manipulations you have the same $\beta_1$ the reasoning remains valid. –  Sep 05 '15 at 16:01
  • user83346 I'm not sure that is correct...or at least I am not convinced: Using some data I have on my hard drive and estimating a model in levels in Stata via OLS gives: GGOW | Coefficient Std. err. t P>|t| [95% conf. interval] LOTH | 1.195524 .0590828 20.23 0.000 1.079074 1.311973 _cons | 11.19726 3.467343 3.23 0.001 4.363275 18.03124 and then estimating a regression in first differences gives: D.GGOW | Coefficient Std. err. t P>|t| [95% conf. interval] LOTH | D1. | .7686487 .0619428 12.41 0.000 .6465622 .8907353 .... and this coefficient (0.769) is *nowhere near* the coefficient in levels (1 – David King Aug 23 '21 at 19:21
0

Take the final Transfer Function and re-express it as a pure right hand side equation. In this form it will be a PDL or ADL. Interpretation will then follow as usual. I implemented that option in AUTOBOX and called it the RIGHT-HAND side. If you post a data set and the model that you wish to use, I will be happy to post the results.

EDITED : TO PRESENT AN ILLUSTRATIVE EXAMPLE TO TEST HYPOTHESIS OF EQUAL COEFFICIENTS:

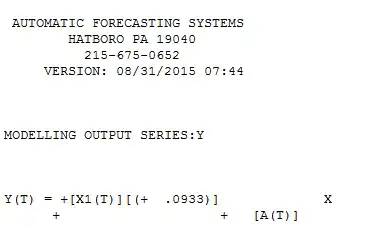
I took the GASX data set (X first then Y)from the Box-Jenklins text available here http://www.autobox.com/stack/GASX.ASC and estimated a Transfer Function on the undifferenced series and obtained enter image description here

I then introduced simple differencing on both Y and X and obtained enter image description here . The hypothesis that the coefficients are the same is rejected. The coefficients are similar but definitely not the same. I then tried to introduce an MA coefficient (near 1.) to complete the algebraic exercise of multiplying through by [1-B] but that didn't reproduce the non-differenced results either.

In summary: The answer is they are different but that may be due to the omittedenter image description here constant term in the undifferenced case.

I decided to simulate two white noise series (X1 and Y1 ) and to estimate an OLS model for them without a constant term and obtained. I then integrated both the X1 and the Y1 white nosie series and obtained two new series (X2 and Y2). Following is the result of an OLS model for X2 AND Y2 [enter image description here][4 The resultant regression coefficient is nearly identical (small variation due to 1 less observation in the X2,Y2 study. Thus I can conclude that the case is proven ( or not rejected) that regression coefficients are comparable. Note that when I introduced a constant in the (X1 versus Y1) the regression coefficient was not the same. Apparently there is a requirement that no constant should be incorporated in the base case (undifferenced) . These findings agree with @f coppens .

IrishStat
  • 27,906
  • 5
  • 29
  • 55
  • I dont follow - transfer function? Can you show what you mean? – B_Miner Sep 03 '15 at 00:00
  • A general transfer function takes the form: Yt=μ+[(ω0−ω1B1−.....−ωsBs)/1−δ1B1−...δrBr)]Xt−b+et where et may have some arima structure – IrishStat Sep 03 '15 at 00:30
  • Do I take it from your answer that the interpretation of the $\beta_{i}$ actually do change with differencing? I am not sure how to construct a transfer function from what I have in my question. – B_Miner Sep 03 '15 at 00:39
  • The βi interpretation when no differencing is in effect is that the level of Y is affected while if differencing is in place the change in Y is affected. – IrishStat Sep 03 '15 at 02:26
  • Look at the link in my question. It seems to say here that the interpretation for a differenced model is exactly the same as the levels. Are you suggesting this is not the case? I am confused by what seems like differences (no pun intended) in answers. – B_Miner Sep 03 '15 at 11:41
  • The interpretation is based upon Yt=β0+β1X1t+β2X2t++...+βpXpt+ . The role of the difference equation is a temporary/working one . – IrishStat Sep 03 '15 at 11:50
  • 1
    So......differencing doesn’t change the interpretation of a regression model? – B_Miner Sep 03 '15 at 11:55
  • Regardless of the differencing (e.g. seasonal)? – B_Miner Sep 03 '15 at 12:28
  • The role of the differencing operators is to transform the data much like a pre-filtering step so that parameter estimation can proceed effectively. Ultimately the interpretation comes from the base (original model), Differencing or pre-whitening in general is to enable efficient identification of the required model form leading to estimates of parameters of that form. – IrishStat Sep 03 '15 at 12:47
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/27727/discussion-between-b-miner-and-irishstat). – B_Miner Sep 03 '15 at 12:55
  • Hi IrishStat. You are too smart in this subject :) I need to dumb it down to a simple level else I worry that I am not interpreting your response properly. So, is it correct for me to say then that the interpretation of the $\beta_{i}$ in a linear regression model DO NOT CHANGE regardless if the dependent and independent variables were all differenced? The interpretation is still in terms of the levels (undifferenced) model? And it doesn't matter if the differencing was a first difference, second difference or a seasonal difference. Am I saying that correctly? – B_Miner Sep 03 '15 at 14:45
  • i can't seem to type a response in the chat session but I can't really accept your last statement/ I suggest we talk via SKYPE or call me on my land line 215-394-8897 in the us – IrishStat Sep 04 '15 at 20:15
  • I dont want to impose like that. When I see you on I will resend the chat invite. Thanks in advance Dave! – B_Miner Sep 04 '15 at 22:40
  • not an imposition at all ... sometimes it is easier to have a dialogue than an infinite number of monologues. , In fact I would prefer it as I speak better than I type. Please call either SKYPE at dave@autobox.com or the landline ..... – IrishStat Sep 05 '15 at 01:19