8

I am doing some research using logistic regression. 10 variables influence the dependent variable. One of the aforementioned is categorical (e.g., express delivery, standard delivery, etc.). Now I want to rank those categories based on the "strength" of their effect on the dependent variable.

They are all significant (small p-value), but I think I can't just use the value of the odds for ranking purposes. I somehow need to figure out, if each category is also significantly different from the other categories. Is this correct?

I read about the possibility of centering the variable. Is this really an option? I do not want the rest of my model to be affected.

Stata output in order to support my comment to @subra's post:

Average marginal effects                          Number of obs   =     124773
Model VCE    : OIM

Expression   : Pr(return), predict()
dy/dx w.r.t. : ExpDel

------------------------------------------------------------------------------
             |            Delta-method
             |      dy/dx   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
ExpDel |   .1054605   .0147972     7.36   0.000     .0798584    .1378626
------------------------------------------------------------------------------
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
Lukas
  • 145
  • 2
  • 10

3 Answers3

1

Since you are interested in ranking the categories, you may want to re-code the categorical variables into a number of separate binary variables.

Example: Create a binary variable for express delivery- which would take the value 1 for express delivery cases and 0 otherwise. Similarly, a binary variable for standard delivery.

For each of these recoded binary variables you can calculate the marginal effects as indicated below:

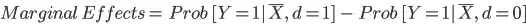
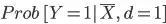Formula

Let me explain a bit on the above equation: lets say d is the re-coded binary variable for express delivery

Formula is the probability of event evaluated at mean when d=1

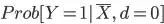Formula is the probability of event evaluated at mean when d=0

Once you calculate the marginal effects for all the categories (re-coded binary variables) you can rank them.

subra
  • 791
  • 3
  • 8
  • Thank you very much for your post, subra. I tried to stick closely to your instructions and accomplished the comand ". margins, dydx(ExpDel)" in stata. You find the output in my original post. Do I Need to run this command over all my categorical (and now binary) variables I'd like to rank and then just need to compare the value dy/dx? The higher the more influence on my dependent variable? Thank you very much! – Lukas Aug 26 '15 at 09:51
  • @ Lukas:Yes, you are correct. In Stata, for discrete data, the 'margins' actually calculates the effect of a discrete change of the co-variate. Therefore, you only have to compare the dy/dx (from margins) for all the categories (now binary). The higher the value the more influence. – subra Aug 26 '15 at 20:25
  • @ subra: Thanks for clarifiying. The above mentioned procedure leads to the same ranking as if I would just rank the respective logit coefficients. I am still not sure about why I may refer to the marginal effects for ranking purposes and not to the logit coefficients. Do you have a source you could recommend for further readings? Furthermore, I am not sure why I should use the above mentioned stata command and not add, e.g., "atmeans" in order to use the means of the other variables for comparison purposes. Thank you very much. – Lukas Aug 27 '15 at 08:16
  • @ Lucas: Yes, you are rite. If you only wanted to rank the predictors, then logit coefficients should be sufficient. I am not clear with your second part of the question. if you are asking why we have to evaluate the marginal effects, please check the following post: http://stats.stackexchange.com/questions/167811/comparing-magnitude-of-coefficients-in-a-logistic-regression/167917#167917 – subra Aug 27 '15 at 15:06
-2

You could fit the logistic regression model using only 1 variable at the time and examine the adjusted R2.

The one explaining most of the variance should have more impact on the model...

I am just guessing, not sure that it is a rigorous solution...

gabboshow
  • 641
  • 6
  • 17
-2

This is a common question with a multitude of answers. The simplest is to use standardized features; the absolute value of coefficients that come back can then loosely be interpreted as 'higher' = 'more influence' on the log(odds). For the most part, using standard scores should not affect your overall results (ROC curve should be the same; confusion matrix should be the same assuming you choose a comparable decision threshold). I usually compute the regression both ways; once using raw scores (to get the prediction equation I will use) and a second time using standardized scores to see which are largest.

As for categorical predictors, I assume (but have not checked) that the same holds true when using normalized predictors.

If you haven't already, you should also consider using regularization: Lasso/ridge/elastic net. This will help weak, irrelevant or redundant features to drop out, leaving you with a more parsimonious model.

HEITZ
  • 1,682
  • 7
  • 15