6

If you open any SVM guide you will see that 1/||w|| is proportional to margin size (which is meant to be maximized by SVM). But how did you get this result?

On the picture below you may see 2 plots. One is $x_{1} = -5x_{2} + 5$ and second is $x_{1} = -5x_{2} - 5$ according to my understanding of comments margin should have size equal to 10 in this case. But if you look at plots you will see its is slightly less than 2.

enter image description here

Marat Zakirov
  • 483
  • 5
  • 14

1 Answers1

8

I assume that you understand that the margin is given by the equation $\langle w,x\rangle+b=\pm k$ where the width of the margin is equal to $2k$ and one has to maximise the width $k$.

Notice that the equation represents a hyperplane with normal vector $w$. Furthermore, if $w$ is a normal vector, then $\lambda w$ is also a normal vector (where $\lambda$ is a scalar). So we can just as well write $\langle \lambda w, x \rangle + b = \pm k$ or $\langle w , x \rangle + \frac{b}{\lambda} = \pm \frac{k}{\lambda}$. So by ''re-scaling" the vector $w$ with a factor $\lambda$ we can reduce the equation to $\langle w, x \rangle + b = \pm 1$.

If you want to compute the distance of a point $x_0$ to a hyperplane (see my answer to Getting distance of points from decision boundary with linear SVM?) than you have to compute

$\frac{| \langle w, x_0 \rangle +b |}{\sqrt{ \langle w,w \rangle}}$. (note that ${\sqrt{ \langle w,w \rangle}}=||w||$). If I take $x_0$ a point on the margin, then is must fullfill the equation of the margin, so $\langle w, x_0 \rangle +b=\pm 1$ so for a point on the margin the distance is equal to $\frac{| \langle w, x_0 \rangle +b |}{\sqrt{\langle w,w \rangle}}=\frac{| \pm 1 |}{\sqrt{\langle w,w \rangle}}$

EDIT: you added the picture and asked an additional question:

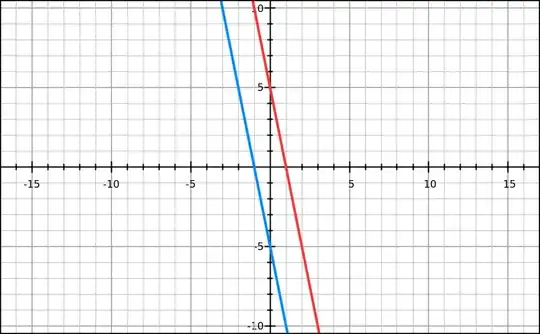
For equation $x_1+5x_2=5$ we see that when $x_1=0$ then $x_2=1$ and for $x_2=0$ we have $x_1=5$, so the $x_1$ axis is vertical and $x_2$ horizontal (you see that when you look for these points on your graph).

The point $(x_1,x_2)=(5,0)$ is on the red line (note that your $x_1$ is vertical) , $w$ is the vector $(1,5)$ and your equation is $x_1+5x_2+0=0$, so you have to compute $\langle w, x \rangle + 0 = 1 \times 5 + 5 \times 0 + 0 = 5$ and divide this by the norm of $w$ which is $\sqrt{1 \times 1 + 5 \times 5} \approx 5.1$, so half the margin is $\frac{5}{5.1}$

EDIT: Added after the question in your comments

The reason for 'eliminating' the $k$ is technical: because of the fact that the normal vector is only known op to a constant, the problem has no unique solution. So either you have to fix the norm of w or you have to fix the k. You could see both cases as choosing a different unit for measuring distances.

Community
  • 1
  • Thank you for answer. Suppose I have 2 dimension case with margins 1*x1 + 1*x2 + 0 = ±1. I say that margin size is equal to sqrt(2) not 2. Why I am not right? – Marat Zakirov Aug 24 '15 at 13:18
  • @Marat Zakirov: you don't have to thank me, it's better to vote for the answer (but only of you like it of course). The answer works in multi-dimensions: $\langle w, x \rangle=\sum_i w_i x_i$, $x$ and $w$ are vectors, $b$ is a scalar. –  Aug 24 '15 at 13:30
  • @user777: thanks (+1), I will edit the answer –  Aug 24 '15 at 13:30
  • I do not enough reputation to vote. Actually there is some misunderstanding. Maybe it will be great if I post some picture. – Marat Zakirov Aug 24 '15 at 13:39
  • @Marat Zakirov: Normally it should be possible to edit yor question and add a picture. I you do that I will see whether I can help you. (Is it impossible to vote for answers on your own question ?) –  Aug 24 '15 at 13:42
  • @f coppens SE said I must have at least 15 points reputation. – Marat Zakirov Aug 24 '15 at 14:03
  • @Marat Zakirov: no problem, I edited the answer, but be carefull when you compute values because your $x_1$ is on the vertical axis. –  Aug 24 '15 at 14:16
  • >>> where the width of the margin is 2k and you have to maximise k. So actually you meant 2k/||w|| ? – Marat Zakirov Aug 24 '15 at 14:26
  • @Marat Zakirov: I see your confusion but the reason is technical: because of the fact that the normal vector is only known op to a constant, the problem has no unique solution. So either you have to fix the norm of $w$ or you have to fix the $k$. You could see both cases as choosing a different unit for measuring distances. –  Aug 24 '15 at 15:04