What is the expected magnitude, i.e. euclidean distance from the origin, of a vector drawn from a p-dimensional spherical normal $\mathcal{N}_p(\mu,\Sigma)$ with $\mu=\vec{0}$ and $\Sigma=\sigma^2 I$, where $I$ is the identity matrix?
In the univariate case this boils down to $E[|x|]$, where $x \sim \mathcal{N}(0,\sigma^2)$. This is the mean $\mu_Y$ of a folded normal distribution with mean $0$ and variance $\sigma^2$, which can be calculated as:
$\mu_Y = \sigma \sqrt{\frac{2}{\pi}} \,\, \exp\left(\frac{-\mu^2}{2\sigma^2}\right) - \mu \, \mbox{erf}\left(\frac{-\mu}{\sqrt{2} \sigma}\right) \stackrel{\mu=0}{=} \sigma \sqrt{\frac{2}{\pi}}$
Since the multivariate normal is spherical, I thought about simplifying the problem by switching to polar coordinates. Shouldn't be the distance from the origin in any direction be given by a folded normal distribution? Could I integrate over all distances, multiply with the (infinitesimal) probability to encounter a sample with that distance (e.g. CDF(radius)-CDF(radius-h), $h \rightarrow 0$) and finally make the leap to more than one dimension by multiplying with the "number of points" on a hypersphere of dimension $p$? E.g. $2 \pi r$ for a circle, $4 \pi r^2$ for a sphere? I feel that this might be a simple question, but I'm not sure how to analytically express the probability for $h \rightarrow 0$.
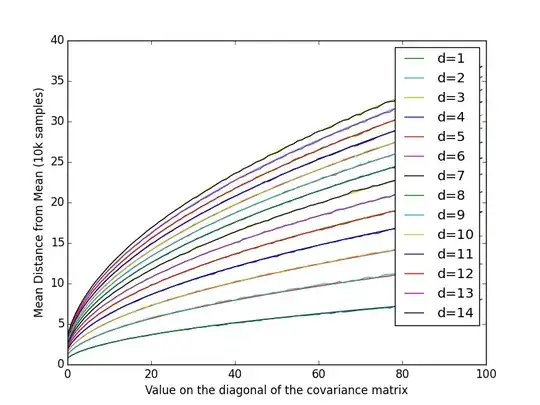
Simple experiments suggest that the expected distance follows the form $c\sqrt{\sigma}$, but I'm stuck on how to make the leap to a multivariate distribution. By the way, a solution for $p \le 3$ would be fine.