receiver operating characteristic (ROC) on a test set

Question

The following image definitely makes sense to me.

Say you have a few trained binary classifiers A, B (B not much better than random guessing etc. ...) and a test set composed of n test samples to go with all those classifiers. Since Precision and Recall are computed for all n samples, those dots corresponding to classifiers make sense.

Now sometimes people talk about ROC curves and I understand that precision is expressed as a function of recall or simply plotted Precision(Recall).

I don't understand where does this variability come from, since you have a fixed number of test samples. Do you just pick some subsets of the test set and find precision and recall in order to plot them and hence many discrete values (or an interpolated line) ?

Answer 1

Short answer

You get different sensitivity/ specificity pairs for every treshhold of your marker variable. If you plot this pairs as points in the ROC plot and connect the points with lines you get the ROC curve.

Explanation with an example

Let's assume you have some binary outcome variable $y$ and you want to classify your cases to $y$ using some marker variable $x$. Here is an other vizualitation than the usual one:

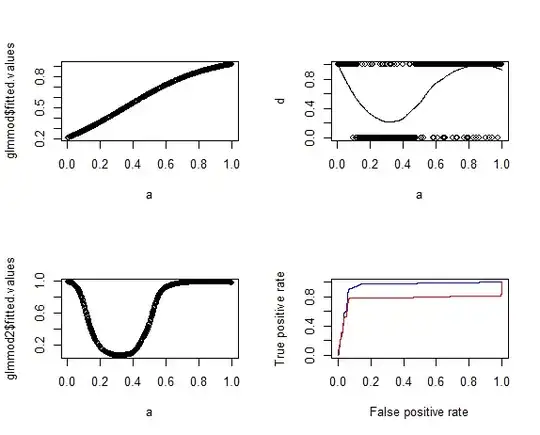
What happens if you set the treshhold at -1? See the following plot:

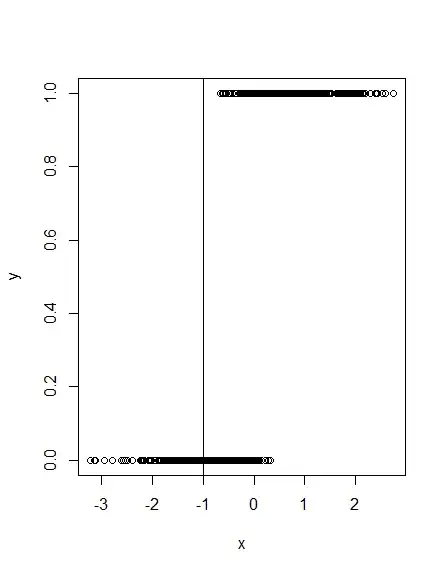
Obviously, this will classify all cases with $y= 1$ correctly, while many cases with $y= 0$ are misclassified. What if you choose another treshhold, say -.5?

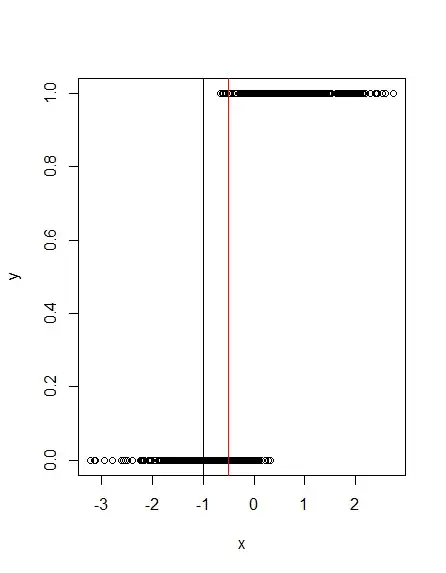
Here, the red line at -.5 shows that a few cases with $y=1$ and quite some cases with $y= 0$ are misclassified. This means, that for every treshhold that you choose you will get different fractions of (in)correctly classified cases of $y= 1$ and $y= 0$. Since the fraction of correctly classified positive cases ($y= 1$) is called sensitivity and the fraction of correctly classified false cases ($y= 0$) is called specificity, it is obvious that you get different sensitivity/ specificity pairs for every treshhold of your marker variable. If you plot this pairs as points in the ROC plot and connect the points with lines you get the ROC curve.

R code

# generate data like here https://stats.stackexchange.com/questions/46523/how-to-simulate-artificial-data-for-logistic-regression/46525
set.seed(666)
x = rnorm(1000)           # some continuous variables 
z = 1 + 7*x        # linear combination with a bias
pr = 1/(1+exp(-z))         # pass through an inv-logit function
y = rbinom(1000,1,pr)  

# make a plot
plot(x, y)
abline(v= -1)
abline(v= -.5, col= "red")

Answer 2

If you're looking for an explanation of ROC, An Introduction to Statistical Learning, can provide a good, brief overview (pages 147-148). Basically, you'll get different True Positive and False Positive rates as you value the threshold value for what you determines a positive.

For a more detailed discussion of model evaluation, I really like the presentation in Applied Predictive Modeling.

Answer 3

Often procedures will have some kind of tuning parameter or cutoff value that you can vary. At different values of this parameter the procedure will produce different sensitivity/specificity. It is this that is plotted by ROC curve

For example in logistic regression where you are trying to do binary classification, the final outcome is a value between 0 and 1. What cutoff should you use to put a value into one category or another? 0.5 seems like a natural choice, but is this the best?