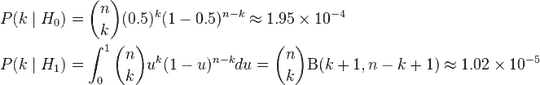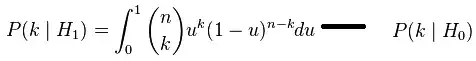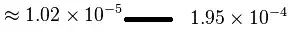0

From Wiki:

enter image description here

where

enter image description here, k is binomially distributed, and I'm not sure about u.

  1. I'm thinking that the second line should be:

enter image description here enter image description here

I mean, if we let X represent the toss of a die, then $P(X = 1, 2, 3, 4, 5) = P(X = 1, 2, 3, 4, 5, 6) - P(X = 6)$ right? Why don't we subtract out $P(k | H_0)$?

Actually, I seem to recall one point doesn't affect value of integral at all, so long as integrand is defined or continuous at that point or something like that, something like:

$\int_{[a,b]} f(x) dx = \int_{[a,b] \setminus \{c\}} f(x) dx \ \forall c \ \in [a,b]$ for some suitable f.

I think that's because $\int_{\{c\}} f(x) dx = 0$.

Then again, $P(k | H_0) = 0$ voids the result at the end of the section.

Is it that $\int_{\{c\}} f(x) dx = 0$ doesn't hold here because we are using Lebesgue integration over counting measure or something? So $\int_{\{0.5\}} \binom{n}{k} (u)^k (1-u)^k du = \binom{n}{k} (0.5)^k (1-0.5)^k du$ kind of like here?

Community
  • 1
BCLC
  • 2,166
  • 2
  • 22
  • 47
  • 1
    What do the thick black dashes in your images mean? Regardless, one way to understand the second integral is that it's really an integral over all $u$ in $[0,1/2)\cup(1/2,1]$--that is, it does not include the value $1/2$. It's still Riemann integrable and you get the same result. – whuber Aug 12 '15 at 16:16
  • @whuber Thanks. They're minuses. Sorry for the confusion. Do we still get the same value because of what was pointed out below? – BCLC Aug 12 '15 at 18:19

1 Answers1

2

You are forgetting what conditioning does. The second line is

$$ P(K=k|H_1) = \int P(K=k|u)p(u|H_1) du $$

where $u$ (should have been $\theta$ on the wiki page given the stated assumption on that page) is assumed to have a uniform distribution over the interval (0,1) and thus this equation is correct.

What you are thinking is that

$$ P(H_1|k) = 1-P(H_0|k). $$

This works because 1) on both sides you are conditioning on the same quantity and 2) $H_0$ and $H_1$ are the only two possibilities. Thus, from the wiki, we could infer that $P(H_1|k) = 1-P(H_0|k) \approx 0.05$.

jaradniemi
  • 4,451
  • 13
  • 25