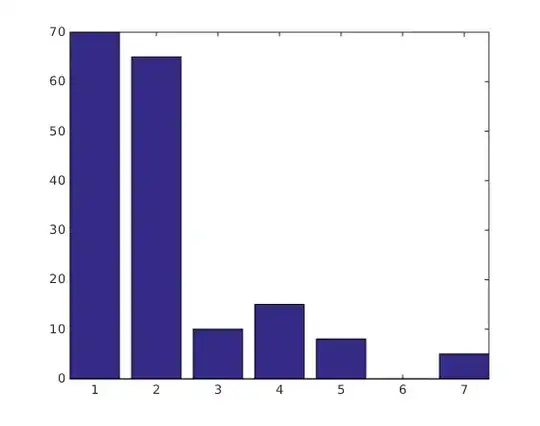
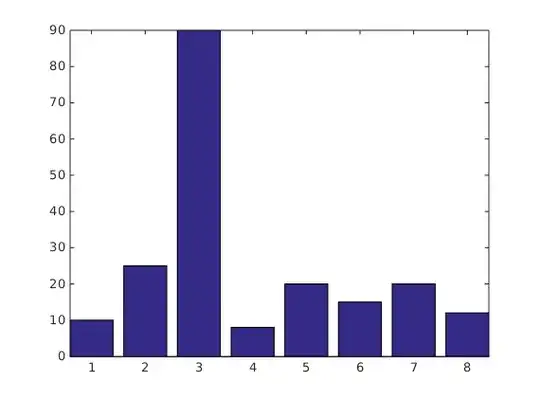
I have a bunch of histogram distributions. In some of the histograms (let's call these Type-A), the initial 2-3 bins are extremely tall compared to the remaining bins. In others, there is no discernible pattern (let's call these Type-B). I would like to differentiate between Type-A and Type-B distributions. Now, Type-A seems like the opposite of heavy-tailed distribution (heavy-headed ?). Is there a way to characterize such distributions ?
Ideally, I would like to accomplish this in such a way that the differentiating measure (between Type-A and Type-B) holds for a reasonable range of histogram bin sizes.
Examples:
Type-A:
Type-B: