How to generate nD point process?

Question

Context:
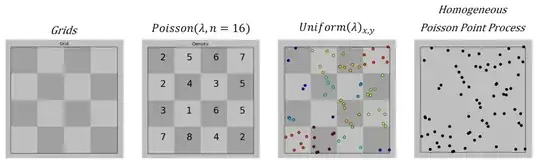
Poisson point processes (PPP) are widely discussed in the literature. In the following figure a framework to generate two-dimensional PPP is demonstrated. First the area being studied (part of space which can be in 1D, 2D, 3D, ..., in our example is a 2D shape i.e., square) is divided into cells (gridding). Second, for each cell a random number n is drawn from a Poisson distribution with density of $\lambda$. Then within each cell n points are uniformly distributed. The resulting point pattern is a homogeneous point process.

Questions:

1. Is the described method correct?
2. If we shuffle the numbers within area, then is it still a valid PPP?
3. Is it valid for further dimensions?

Please check whether the following steps are the same as I illustrated.

note Please read the following invaluable answers and comments which are appreciable. I don't repeat them here. However I put a confusing point here hopefully to be solved by a gentle explanation.

The second point is if we do realization only once then why should we call it Poisson where it is simply a uniform-random-values?

Answer 1

You don't need to grid. You could just draw a Poisson count, $n$, for the total number of points and then simulate $n$ iid points uniform on the region. For a square, you can draw $x_i$ and $y_i$ as independent uniforms. (For a more complex region, the simplest thing would be to embed it in a square, simulate for the square, and then just keep the points in the target region.)

The same thing can be done in higher dimensions. You draw the count from a Poisson with mean $\lambda V$ where $\lambda$ is the rate for the Poisson process and $V$ is the volume of the region, and then simulate that number of iid uniform points from the region.

And so 1: yes, 2: yes (if the grid regions are the same area), and 3: yes.

Answer 2

@Karl gave a good answer but it deserves an explanation.

A homogeneous Poisson point process (or "complete spatial randomness," CSR) is determined by two intuitive properties:

1. The probability that a point will be located within a small region $dA$ is directly proportional to $dA$ (up to second order in the hypervolume of $dA$). Note that this immediately implies the expected number of points in any finite region of hypervolume $A$ is proportional to $A$.

2. The points are located independently of each other.

Assuming the points introduced within each cell are done so independently, using a Poisson distribution of counts in each cell assures overall independence. To check (1), we lose no generality by assuming $dA$ is wholly located within a grid cell (because the probability that it straddles two cells is vanishingly small). That reduces the check to verifying that points are generated with the same intensity within the cells. Using a Poisson distribution of counts with expectation proportional to each cell's hypervolume assures this, as noted in (1).

This argument is independent of dimension. In fact, it would apply to any finite dimensional manifold with a volume form (such as the surface of a sphere in 3D) in which a region has been partitioned into measurable "cells" of arbitrary shape. The reason for using a grid, of course, is that grid cells can be addressed in $O(1)$ computational time and it's simple to generate random points within a rectangular region (merely by generating random coordinates within it). If, as a preliminary matter, an irregular region is preprocessed to identify the cells it contains, this leads to a computationally efficient way to simulate a CSR process. In higher dimensions the preprocessing for an arbitrary or complex region could be messy and time-consuming, but for simply defined manifolds and regions within them (such as spheres or their boundaries) there's no problem.