Which unsupervised classification method to use next if hierarchical clustering gave bad results?

Question

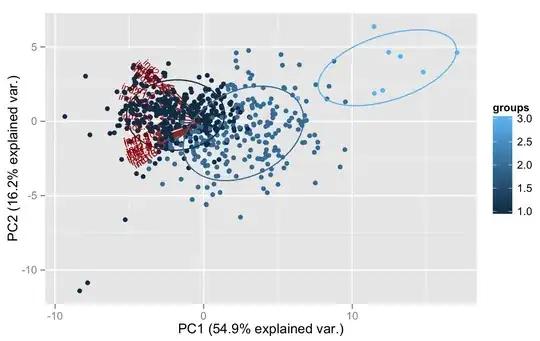
Purposes

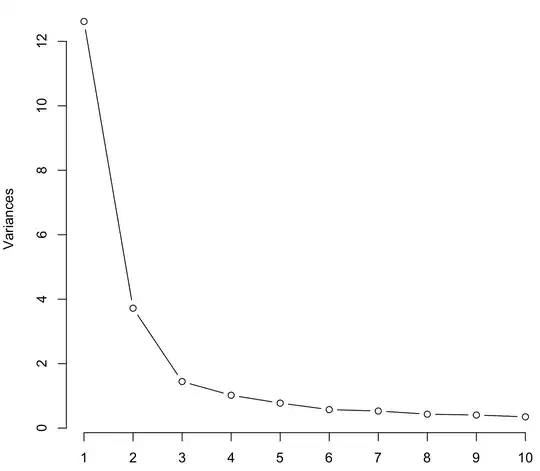
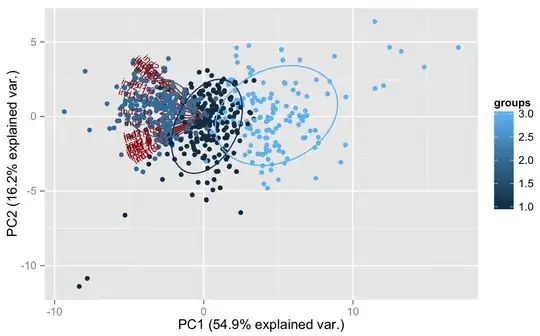
I need to perform a classification of weather stations taking into account the characteristics of intra-annual variability of some two climate indicators. There are 613 sites with monthly averaged data, so the input array has shape 613 x 24.

The seasonal distribution visualized for each indicator separately is shown below:

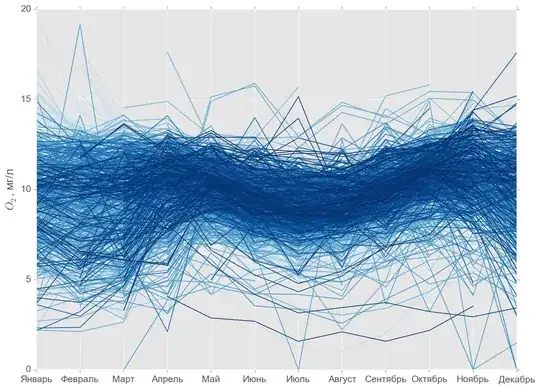
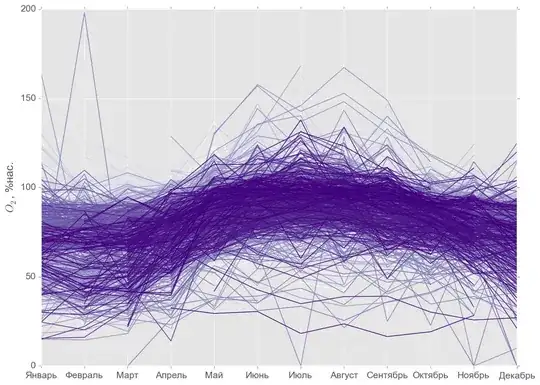
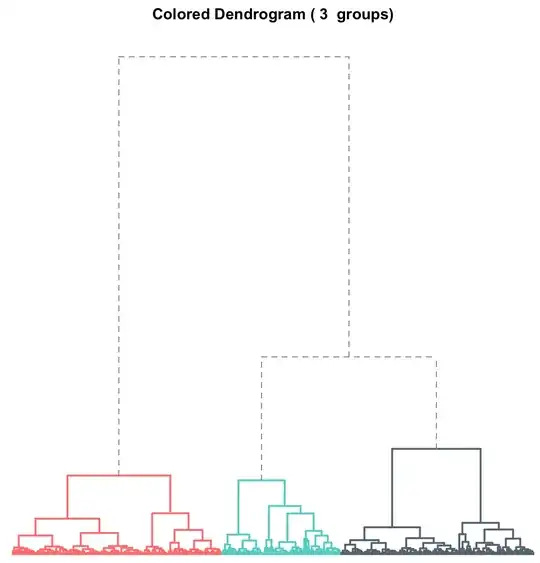
Usually it's possible to find dense groups of weather stations with similar intra-annual variations of indicators. Since there are a lot of classification (separation) methods, the most optimal one should be discovered and approved.

Methodology

Classification method: the hierarchical clustering methods seem to be a default solution for this case. I chose Ward and Complete Linkage methods, and the latter one was used with about 20 different metrics.

Classes amount: $1 \leq k \leq 50$

Estimation method: the quality of classification was estimated with the combination of $I_{r}$ (average intraclass dispersion measure) and $z_{r}$ (average element concentration measure) functions: $$F(k)=I_{r}\cdot\frac{1}{z_{r}}\rightarrow min$$ $$I_{r}^{(k)}=\left [ \frac{1}{k}\sum_{i=1}^{k}\frac{1}{n_{i}}\sum_{x_{p},x_{q}\in S_{i}}d_{pq}^{r}\right ]^{\frac{1}{r}}$$ $$z_{r}^{(k)}=\left [ \frac{1}{k}\sum_{i=1}^{k} \left ( \frac{n_{i}}{k}\right )^{r} \right ]^{\frac{1}{r}}$$ where $k$ is selected amount of classes, $n_{i}$ is amount of elements in a particular class, $r$ is exponent value (equal to 2 in my case), $S_{i}$ is a particular class for the given separation and $\sum_{x_{p},x_{q}\in S_{i}}d_{pq}^{r}$ is a sum of euclidean distances (raised to the $r$) between the elements of a particular class (from Мандель И. Д. Кластерный анализ. М.: Финансы и статистика, 1988. 176 с.).

$I_{r}$ characterizes the intraclass variation and it is a decreasing function of $k$. $\frac{1}{z_{r}}$ inhibits the tendency toward excessive detalization and increases with $k$. These opposite trends are "balanced" in quality functional $F(k)$. So the idea is to find the value $k$ corresponding to the global minimum of $F(k)$.

Results

Consider the $F(k)$ curves for different methods and metrics:

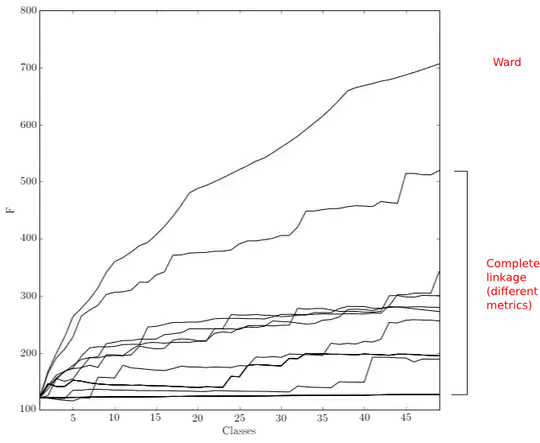
It seems that:

1. Ward method unexpectedly provided the worst results;
2. Global minimum ($k = 5$, complete linkage, chebyshev distance) is very close to the minimum ($k = 1$) of the most of the $F(k)$ curves. Does it mean that it's worth to leave this dataset as it is with no subclasses distinguished?
3. The separation corresponding to the global minimum is degenerated because it provides one huge class with more than 99% of members and four one-element classes.

Question This short research suggests the idea of the absence of subclasses in the discussed dataset. But probably this case is just lying out of the scope of hierarchical clustering methods. There should be other unsupervised learning techniques that can confirm or deny this hypothesis.

Please share your experience and feel free to try this dataset on your own. Any help will be appreciated (especially Python solutions).

Answer 1

I loaded your data into R and applied hierarchical clustering with Ward's method, which gave 3 clean cut clusters for your stations (Fig.1). Then I applied Principal Component Analysis on the scaled data which revealed that 71% of the information is explained by the first two components (Fig.2). A biplot of the first two components shows you how months (direction of vectors in the plot) correlate to stations (scattered points) and to each other (Fig.3). I created a response vector based on the dendrogram of Fig.1 in order to see if the output of Hierarchical clustering is reflected in the principal component scatter plot of Fig.3. It comes out that the 3 clusters appear next to each other (Fig.4). I repeated the whole process using Complete Linkage and it gave me two main clusters instead of three (final result in Fig.5).

These are pretty good results and it doesn't look like you need another method. I guess this is not in agreement with what you found but I hope it helps.

Fig.1

Fig.2

Fig.3

Fig.4

Fig.5

Answer 2

You could try non-hierarchical partitioning.

If you're willing to play in R, you could try package optpart. You'll find a variation of k-means, pam (see Kaufman & Rousseeuw, 1990), as well as two methods of non-hierarchical partitioning, OPTPART and OPTSIL, available. http://cran.r-project.org/web/packages/optpart/optpart.pdf .

Functions silhouette and stride additionally help you decide on the proper number of partitions. These methods can potentially be used (with some modification) for hierarchical clustering methods as well.

A final method to look into is ISODATA (though I admittedly know little about it)

I don't think Dave Roberts has extended OPTPART in any way to Python, but I'm sure some version of pam can be utilized in python with little to no effort. OPTPART usually creates the best partitions for me, so it might be worth looking into. In the end, I'm not sure these methods will necessarily help you any better but, at the very least, they'll provide you with a handful of additional (often overlooked) clustering methods to try.

Hope this helps!