0

A professor in one of my graduate statistics courses once said, when briefly reviewing simple linear regression: "I would never EVER fit a line to fewer than 8-10 data points, it would make me feel...rather uncomfortable." Many of us would agree, as evidenced by "rules of thumb" suggested previously on CV here, here, and here for regression (i.e., "10 samples per covariate").

A regression line like this one ($n$ = 10) might represent this "minimum comfort level":

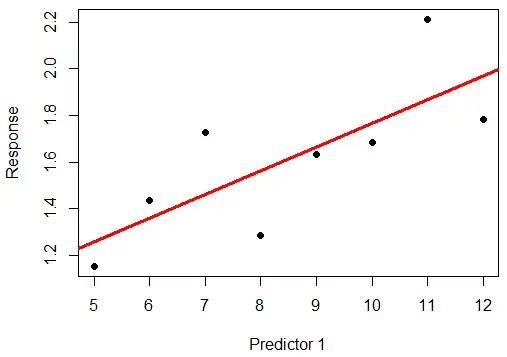
Simple linear regression, n=10

Naturally, our level of confidence in the relationship between Predictor 1 and Response would rise if we had 10 repeated samples at each x-value (for $n$ = 100):

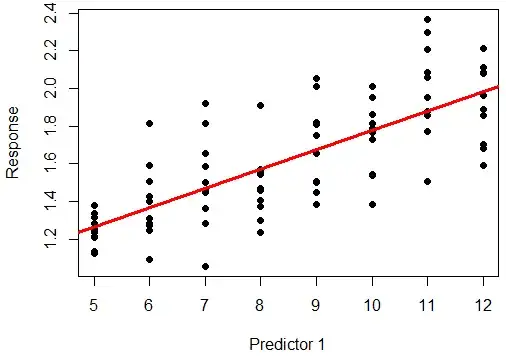
Simple linear regression, n=100

Now, suppose we have a second predictor and want to fit a plane $y$ = $\beta_0$ + $\beta_1$$x_1$ + $\beta_2$$x_2$ + $e$ or even a non-linear interaction $y$ = $\beta_0$ + $\beta_1$$x_1$ + $\beta_2$$x_2$ + $\beta_3$$x_1$*$x_2$ + $e$. Like the example above, suppose we have $n$ = 100, and these 100 samples are repeated 10 times at 10 "unique" predictor values (in this case, 10 unique $x_1$-$x_2$ combinations). Therefore, we have a relatively large sample size ($n$ = 100) for a relatively small number of predictors $n$ = 2, which, given our rule of thumb, would be generally acceptable.

(Left, linear plane; Right, non-linear surface):

Linear planeNon-linear surface

My questions are:

  1. Would repeated samples ("stacking" at the unique $x_1$-$x_2$ combos) improve your confidence in the fit of a plane (as they did in the fitting of a line), given that these samples do not appear to give us more information about un-sampled locations on the plane? Why or why not?
  2. Given your response to question 1, would you "feel comfortable" fitting an interaction term $x_1$*$x_2$, as I have shown in the graph above (right)?

I look forward to discussion.

Community
  • 1
Gavin M. Jones
  • 87
  • 1
  • 12
  • If you feel it makes sense with a single predictor, why wouldn't it with two? – dsaxton Jul 20 '15 at 04:09
  • @dsaxon my concern is that there are few unique values for predictors. Consider a more extreme example where we still have n=100 but only 5 "unique" predictor values instead of 10 as shown above. In my mind, it would be treacherous to predict a surface, especially a non linear one, when I have very little data forming the remainder of the surface. – Gavin M. Jones Jul 20 '15 at 04:14
  • I suppose it could be an issue in much higher dimension where the points observed would represent a more "sparse" sample in terms of distances between points. – dsaxton Jul 20 '15 at 04:25
  • Furthermore, since the "stacked" samples are essentially sub-samples, I wonder if it would be equivalent to take the mean of each "stack" before fitting the plane? In one sense, this would give us only n = 10 data points for 2-3 predictors. – Gavin M. Jones Jul 20 '15 at 12:25
  • 1
    What you remember your professor saying reflects an overly narrow understanding of regression and its uses. *Three* points would be just fine in many circumstances where the assumptions have been independently verified (linearity; normality, independence, and homoscedasticity of errors; accurate measurement of the independent variable). This, and your allusion to "unsampled locations," suggests you really want to explore issues of model selection and *prediction* rather than regression sample sizes or rules of thumb. – whuber Jul 20 '15 at 12:28
  • @Whuber - all things being equal, if you did not have carefully controlled linearity, normality, stationarity, measurement capability - what then? Mathematically all bets are off, right? What about something between the two? There are varying degrees of data management. If you picked 100 "canonical" data sets comparable in legacy with Fischer Iris, or the other items from the R 'datasets' package, and you look at their level of control, what sort of sampling is required to make a credible fit and conclusions? They are not all immaculate, some are probably pretty bad. What is the median? – EngrStudent Jul 20 '15 at 12:45
  • @GavinM.Jones - you want to have enough samples so that you can adequately measure the uncertainty in the parameters of your model. I would call that the minimum for someone in industry, who is paid for their results. If you cannot quantify the model covariance given model and data, then there is a fundamental problem. – EngrStudent Jul 20 '15 at 12:49
  • 1
    @GavinM.Jones About taking the mean before fitting, this isn't equivalent because the least squares fit would change in general (just imagine the samples at the different points being heavily unbalanced, for instance). But probably more importantly, there's more information in an average than a single observation, so it isn't really correct to think of this as only 10 data points. – dsaxton Jul 20 '15 at 13:26
  • 2
    @Engr Questions about the "median" or any other property of a collection of datasets are rarely relevant to the problem one currently faces. This is not a mathematical question: it's a statistical one, and it has to be answered within a context that includes whatever theory is believed to apply, any prior information, the costs of collecting data, and the objectives of the exercise. Blindly following rules of thumb, with absolutely no thought or discretion--"I would never EVER..."--will surely be a costly mistake for some people in some circumstances. – whuber Jul 20 '15 at 14:16
  • @whuber - Operating without blind rules is not the same as proper execution, and also results in costly mistakes. This conversation has some analogy to "should planned parenthood give teenagers free birth control products" because it is about mitigating risk in the presence of (sometimes highly) imperfect decision making. Perhaps the question behind the question is "how do we minimize costly mistakes in the presence of dubious quality decision making"? One answer, possibly a poor one, is lower complexity guidelines that reduce risk - aka heuristics. What do you think is the right approach? – EngrStudent Jul 20 '15 at 15:46

0 Answers0