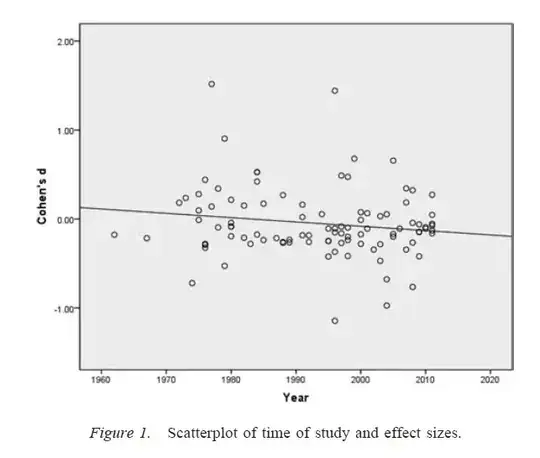
Your concern is exactly the concern that underlies a great deal of the current discussion in science about reproducability. However, the true state of affairs is a bit more complicated than you suggest.
First, let's establish some terminology. Null hypothesis significance testing can be understood as a signal detection problem -- the null hypothesis is either true or false, and you can either choose to reject or retain it. The combination of two decisions and two possible "true" states of affairs results in the following table, which most people see at some point when they're first learning statistics:
Scientists who use null hypothesis significance testing are attempting to maximize the number of correct decisions (shown in blue) and minimize the number of incorrect decisions (shown in red). Working scientists are also trying to publish their results so that they can get jobs and advance their careers.
Of course, bear in mind that, as many other answerers have already mentioned, the null hypothesis is not chosen at random -- instead, it is usually chosen specifically because, based on prior theory, the scientist believes it to be false. Unfortunately, it is hard to quantify the proportion of times that scientists are correct in their predictions, but bear in mind that, when scientists are dealing with the "$H_0$ is false" column, they should be worried about false negatives rather than false positives.
You, however, seem to be concerned about false positives, so let's focus on the "$H_0$ is true" column. In this situation, what is the probability of a scientist publishing a false result?
Publication bias
As long as the probability of publication does not depend on whether the result is "significant", then the probability is precisely $\alpha$ -- .05, and sometimes lower depending on the field. The problem is that there is good evidence that the probability of publication does depend on whether the result is significant (see, for example, Stern & Simes, 1997; Dwan et al., 2008), either because scientists only submit significant results for publication (the so-called file-drawer problem; Rosenthal, 1979) or because non-significant results are submitted for publication but don't make it through peer review.
The general issue of the probability of publication depending on the observed $p$-value is what is meant by publication bias. If we take a step back and think about the implications of publication bias for a broader research literature, a research literature affected by publication bias will still contain true results -- sometimes the null hypothesis that a scientist claims to be false really will be false, and, depending on the degree of publication bias, sometimes a scientist will correctly claim that a given null hypothesis is true. However, the research literature will also be cluttered up by too large a proportion of false positives (i.e., studies in which the researcher claims that the null hypothesis is false when really it's true).
Researcher degrees of freedom
Publication bias is not the only way that, under the null hypothesis, the probability of publishing a significant result will be greater than $\alpha$. When used improperly, certain areas of flexibility in the design of studies and analysis of data, which are sometimes labeled researcher degrees of freedom (Simmons, Nelson, & Simonsohn, 2011), can increase the rate of false positives, even when there is no publication bias. For example, if we assume that, upon obtaining a non-significant result, all (or some) scientists will exclude one outlying data point if this exclusion will change the non-significant result into a significant one, the rate of false positives will be greater than $\alpha$. Given the presence of a large enough number of questionable research practices, the rate of false positives can go as high as .60 even if the nominal rate was set at .05 (Simmons, Nelson, & Simonsohn, 2011).
It's important to note that the improper use of researcher degrees of freedom (which is sometimes known as a questionable research practice; Martinson, Anderson, & de Vries, 2005) is not the same as making up data. In some cases, excluding outliers is the right thing to do, either because equipment fails or for some other reason. The key issue is that, in the presence of researcher degrees of freedom, the decisions made during analysis often depend on how the data turn out (Gelman & Loken, 2014), even if the researchers in question are not aware of this fact. As long as researchers use researcher degrees of freedom (consciously or unconsciously) to increase the probability of a significant result (perhaps because significant results are more "publishable"), the presence of researcher degrees of freedom will overpopulate a research literature with false positives in the same way as publication bias.
An important caveat to the above discussion is that scientific papers (at least in psychology, which is my field) seldom consist of single results. More common are multiple studies, each of which involves multiple tests -- the emphasis is on building a larger argument and ruling out alternative explanations for the presented evidence. However, the selective presentation of results (or the presence of researcher degrees of freedom) can produce bias in a set of results just as easily as a single result. There is evidence that the results presented in multi-study papers is often much cleaner and stronger than one would expect even if all the predictions of these studies were all true (Francis, 2013).
Conclusion
Fundamentally, I agree with your intuition that null hypothesis significance testing can go wrong. However, I would argue that the true culprits producing a high rate of false positives are processes like publication bias and the presence of researcher degrees of freedom. Indeed, many scientists are well aware of these problems, and improving scientific reproducability is a very active current topic of discussion (e.g., Nosek & Bar-Anan, 2012; Nosek, Spies, & Motyl, 2012). So you are in good company with your concerns, but I also think there are also reasons for some cautious optimism.
References
Stern, J. M., & Simes, R. J. (1997). Publication bias: Evidence of delayed publication in a cohort study of clinical research projects. BMJ, 315(7109), 640–645. http://doi.org/10.1136/bmj.315.7109.640
Dwan, K., Altman, D. G., Arnaiz, J. A., Bloom, J., Chan, A., Cronin, E., … Williamson, P. R. (2008). Systematic review of the empirical evidence of study publication bias and outcome reporting bias. PLoS ONE, 3(8), e3081. http://doi.org/10.1371/journal.pone.0003081
Rosenthal, R. (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638–641. http://doi.org/10.1037/0033-2909.86.3.638
Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2011). False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychological Science, 22(11), 1359–1366. http://doi.org/10.1177/0956797611417632
Martinson, B. C., Anderson, M. S., & de Vries, R. (2005). Scientists behaving badly. Nature, 435, 737–738. http://doi.org/10.1038/435737a
Gelman, A., & Loken, E. (2014). The statistical crisis in science. American Scientist, 102, 460-465.
Francis, G. (2013). Replication, statistical consistency, and publication bias. Journal of Mathematical Psychology, 57(5), 153–169. http://doi.org/10.1016/j.jmp.2013.02.003
Nosek, B. A., & Bar-Anan, Y. (2012). Scientific utopia: I. Opening scientific communication. Psychological Inquiry, 23(3), 217–243. http://doi.org/10.1080/1047840X.2012.692215
Nosek, B. A., Spies, J. R., & Motyl, M. (2012). Scientific utopia: II. Restructuring incentives and practices to promote truth over publishability. Perspectives on Psychological Science, 7(6), 615–631. http://doi.org/10.1177/1745691612459058