relation between probability and probability density function

Question

According to this link: PDF

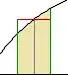
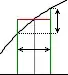
To translate the probability density $ρ(x)$ into a probability, imagine that $I_x$ is some small interval around the point $x$. Then, assuming $ρ$ is continuous, the probability that $X$ is in that interval will depend both on the density $ρ(x)$ and the length of the interval:

$Pr(X∈I_x)≈ρ(x) × $ Length of $I_x$

We don't have a true equality here, because the density $ρ$ may vary over the interval $I_x$. But the approximation becomes better and better as the interval $I_x$ shrinks around the point $x$, as $ρ$ will be come closer and closer to a constant inside that small interval.

My questions are:

1. Why is $Pr(X∈I_x)≈ρ(x) ×$ Length of $I_x$? Shouldn't it simply be $Pr(x∈A)=\int_{A}ρ(x)dx$?

2. Why as $I_x$ shrinks around the point $x$, will $ρ$ become closer and closer to a constant inside that small interval? Is it because as we reduce the interval, we zero in on $x$?

3. How and why the density $ρ$ may vary over the interval $I_x$?

Answer 1

1. Yes; the description is however useful for mathematically naive audience (perhaps an audience more naive than you); it's simply motivating an understanding like the one you already have, by using a concept akin to that of one term in a middle Riemann sum.

   $\qquad\qquad$

   If the audience has had exposure to the mean value theorem, or would at least be able to understand it, that would be a better motivation.

2. Imagine we're dealing with a sufficiently "nice" pdf, say one that's Lipschitz continuous. Then in a direct sense, as the interval in $x$ gets smaller, the interval in $f$ must also get smaller.

   $\qquad\qquad$

3. It's not quite clear what you're after here. Clearly for "2." to hold we must have some restrictions on the way $f$ behaves, but density functions are not necessarily required to be Lipschitz continuous.

   However, we needn't overly interpret the meaning of the phrases in question; it's intended as motivation in building a naive understanding of the relationship between density and probability, not proof of anything.

Answer 2

Another observation is that this is almost a restatement of the definition of the density function. Recall that $$ f(x) \equiv \lim_{\delta \downarrow 0} \frac{P(x \leq X \leq x + \delta)}{\delta} $$ which means $\delta f(x) \cong P(x \leq X \leq x + \delta)$ for sufficiently small $\delta$.