3

Suppose $100p\%$ of babies born are male. Sometimes one reads that $p\approx 0.505$ or something like that. If a couple has $n$ children, it is often assumed that the sex of each child is independent of those of the children born earlier to the same couple.

Has that hypothesis of independence been tested? What can be said based on data, about the nature of the dependence?

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
Michael Hardy
  • 7,094
  • 1
  • 20
  • 38
  • 1
    Identical twins (triplets, etc.) discredits independence right off the bat. – Mark L. Stone Jul 10 '15 at 20:21
  • @MarkL.Stone : True, but the more interesting question is about independence within families without such multiple births. – Michael Hardy Jul 10 '15 at 20:29
  • Some of us explicitly [do *not* make this assumption](http://stats.stackexchange.com/a/93890/919). It's not hard to search the Web for such studies. One early hit I found is at http://phys.org/news/2008-12-boy-girl-father-genes.html. This issue seems off-topic here, because it concerns a matter of biology and not statistics or even statistical analysis. What statistical question do you have in mind? – whuber Jul 10 '15 at 21:05
  • 1
    The existence of multiple births within a family is itself not independent. Pre-in vitro fertilization, answer was somewhat different, and on the verge of changing with selection and manipulation techniques. Also distribution of sex conceived is not the same as those born due to abortions based on sex of baby, which didn't exist in any significant numbers prior to ultrasound. Etc. Of course you can say none of this counts, in which case just assume anything you want, and under those assumptions, anything you want can be true. – Mark L. Stone Jul 10 '15 at 23:14
  • 1
    I do not have an answer, but this reminds me of a recent article on the gambler's fallacy and how hard it is to unlearn it with finite samples: http://poseidon01.ssrn.com/delivery.php?ID=832089093027127102115103093108080031050054000027004013125083086105110110110065122110107058000012017055113127089098089071118102062040012017050012011069116018091085076009069034104114117010099064100068020075122097081106067088069111092094086077080079099&EXT=pdf&TYPE=2 – Brash Equilibrium Jul 10 '15 at 23:53

1 Answers1

1

The hypothesis have been tested, for instance this interesting biorxiv paper: An association between sexes of successive siblings in the data from Demographic and Health Survey program which analysis millions of births. A few quotes:

A formal modelling demonstrated that sexes of the children were dependent on three kinds of sex ratio variation: a variation between families (Lexian), a variation within a family (Poisson) and a variation contingent upon the sex of preceding sibling (Markovian).

Turpin and Schutzenberger analyzed a sample from France (14,230 families) and observed positive correlation between sexes of successive siblings. Unlike Gini, they hypothesized that the correlation could be explained by an influence of one birth on the following birth. This idea was supported by the fact that the interval between births of same sex siblings was on average shorter than for opposite sex siblings (however, Gini interpreted this result in favor of his “reversal of predisposition” explanation).

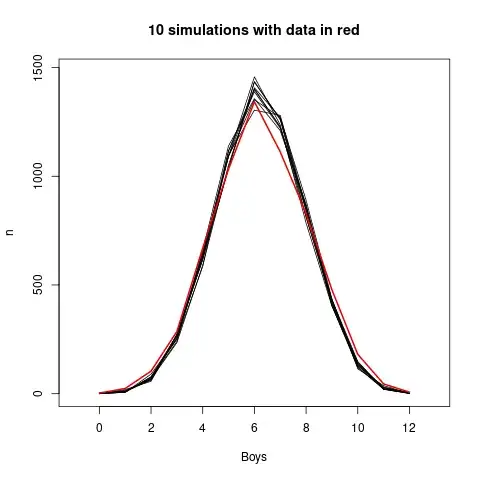
A classic dataset of interest is the Saxony dataset of about 6000 12-child families, which was used as example here: How do I compute the estimated values of x for a beta-binomial distribution? If there is variation in $p$ between families, the distribution of number of boys will not be binomial, maybe beta-binomial could fit closer. Below is a plot from simulations based on a binomial model, with the Saxony data overlaid:

enter image description here

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
  • 1
    These sample sizes are small compared to what would be found in national census data. If the effect is small, it might take a census to detect it. – Michael Hardy Oct 29 '21 at 17:03