Calculating parameters for a mixture of beta distributions

Question

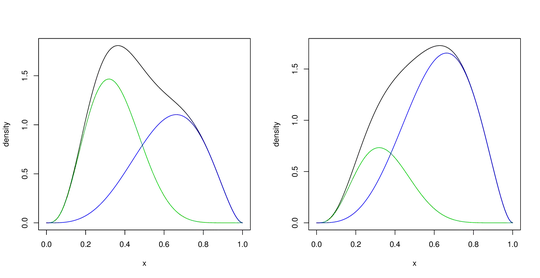
I have two beta distributions with known parameters:

x <- seq(0,1.0,0.01)   

mu1 <- 0.348       
mu2 <- 0.619      
var1 <- 0.017
var2 <- 0.028

alpha1 <- ((1-mu1)/var1 - 1/mu1)*mu1^2  # constrained to be greater than 1
beta1 <- alpha1*(1/mu1 - 1)
alpha2 <- ((1-mu2)/var2 - 1/mu2)*mu2^2  # constrained to be greater than 1
beta2 <- alpha2*(1/mu2 - 1)

betad1 <- dbeta(x, alpha1, beta1)
betad2 <- dbeta(x, alpha2, beta2)

plot(x,betad1,ylab="density",col='green')
points(x,betad2,col='blue')

(I didnt manage to insert my graphical outpout but it should be straighforward to plot)

I would like to do two things,

1. Plot the mixture distribution formed by betad1 and betad2
2. Find a set of single beta and alpha parameters (or mu and sigma) giving the best representation of this mixture.

For point number 1, I tried the method shown in this post, which is very useful but mixdist does not allow for beta distributions to be used: is there an similar package for a beta densities mixture?

For point number 2, I believe the best thing I can do is to "approximate" the bimodal mixture with a unimodal beta pdf, and calculate its parameters. I am unsure what is the best approach for this. Alternatively, is there there a standard way to characterize a mixture with a single set of parameters?

Answer 1

As for item 1 you still need to specify the mixture weights, say a 50:50 weighting:

plot(x, 0.5 * betad1 + 0.5 * betad2, ylab = "density", type = "l")
lines(x, 0.5 * betad1, col = 3)
lines(x, 0.5 * betad2, col = 4)

Or as a different example with 25% and 75% weights, respectively:

plot(x, 0.25 * betad1 + 0.75 * betad2, ylab = "density", type = "l")
lines(x, 0.25 * betad1, col = 3)
lines(x, 0.75 * betad2, col = 4)

Possibly, the betareg package will also be useful for you. This supports estimation of finite mixtures of beta-distributed variables in function betamix(). See: http://www.jstatsoft.org/v48/i11/.