Testing for cluster structure in one dimension

Question

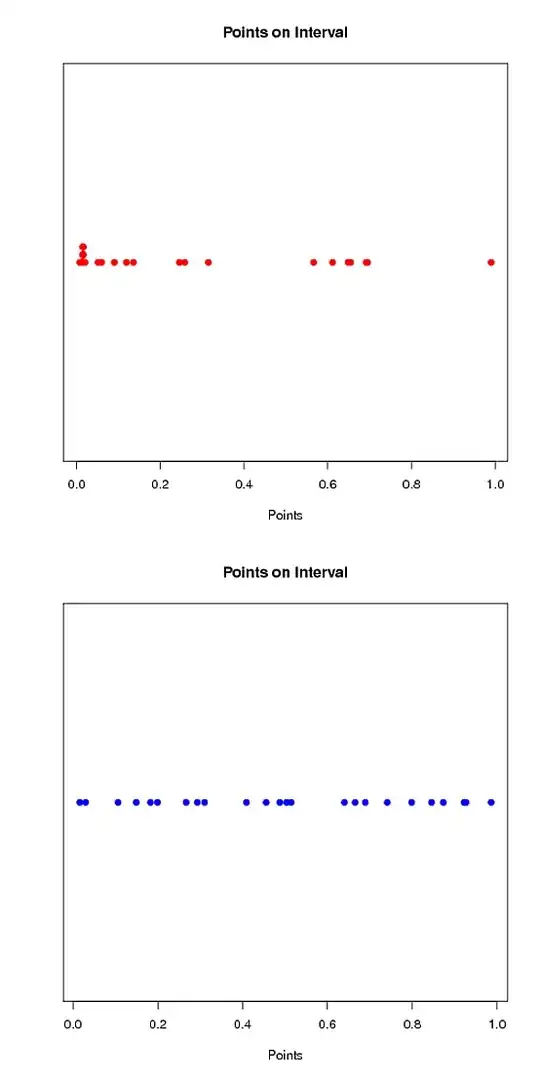
I have a set of points along an interval. What is the best significance test to measure clustering of the points in the interval (deviation from a uniform distribution)?

I've added two examples below - clearly by visual inspection, the red series is clustered while the blue series is more evenly distributed across the interval. I'm looking for a significance test to identify this clustering.

I have attempted to use a number of tests including the KS-test, but this has problems with points in the middle v. at the beginning and end (see: KS test for Uniformity)

A significant limitation here is the number of data points (most likely cannot implement a chi-squared test).

Here are the example sets:

Example Set 1:

[1] 0.007257242 0.010597715 0.010633415 0.011403509 0.014274786 0.014274786
[7] 0.014601183 0.014611383 0.014616483 0.014621583 0.014647083 0.014647083
[13] 0.014647083 0.014692982 0.014692982 0.014703182 0.014703182 0.014718482
[19] 0.014738882 0.014743982 0.014759282 0.014764382 0.014764382 0.014789882
[25] 0.014810282 0.014810282 0.014866381 0.014866381 0.014866381 0.014866381
[31] 0.014866381 0.014871481 0.014871481 0.014871481 0.014876581 0.014876581
[37] 0.014891881 0.014891881 0.014891881 0.014891881 0.015070379 0.015070379
[43] 0.015146879 0.015146879 0.015151979 0.015151979 0.015151979 0.015162179
[49] 0.015172379 0.015172379 0.015177479 0.015177479 0.015345777 0.015427377
[55] 0.015427377 0.020063239 0.051172991 0.059077927 0.090044880 0.118604651
[61] 0.135638515 0.245542636 0.258465932 0.314723582 0.566289270 0.611383109
[67] 0.648434313 0.648434313 0.654238066 0.691605467 0.695608935 0.990172379

Example Set 2:

[1] 0.01579036 0.01579036 0.02972629 0.10616355 0.10616355 0.14897223
[7] 0.18280039 0.19935524 0.26667997 0.29327766 0.40871955 0.40871955
[13] 0.45590335 0.48782180 0.50356611 0.50356611 0.51465283 0.64006079
[19] 0.66558696 0.68946746 0.68946746 0.74137026 0.79837890 0.84520041
[25] 0.87293410 0.87293410 0.92225480 0.92225480 0.98610399

Answer 1

The distribution of intervals between order statistics of a uniform distribution is exponential. Therefore, apply any distributional test you like to those intervals. But before you do that, draw a QQ plot of them:

qq.unif <- function(x, ...) {
  dx <- diff(sort(x))
  n <- length(dx)
  p <- -log(1 - (1:n) / (n+1))
  plot(sort(dx), p, ...)
}
par(mfrow=c(1,3))
qq.unif(x, main="x")
qq.unif(y, main="y")
qq.unif(runif(100), main="Uniform"

(This R code presumes the data arrays are named x and y.) Its output shows their QQ plots along with a reference plot obtained from $100$ iid uniform variates:

Uniform variates will appear to line up along the main diagonal. Deviations from that diagonal indicate deviations from uniformity:

• The x dataset is far from uniform: it contains too many small differences or too few large ones.

• The y dataset is close to uniform. But look at the stack of values at $0$: these ties are evidence of subtle non-uniformity.

• The random dataset is close to uniform. Drawing a few plots like this will indicate how much deviation to expect when the data should be considered uniform.

This graphical approach is far more revealing and useful than any single statistical test would be.

Answer 2

Your problem is similar if not identical to determining how many different means or unique distributions exist in a given set of numbers. We observe the data and wish to generate hypothesis regarding the number of distribution without any prior assumptions. Consider a simple case where we have a series (free of auto-correlation) of say 20 values and a following series (free of auto-correlation) of 20 values BUT having a different mean. If we sort the 40 values from low to high and analyse it as if this new series was a time series of consecutive values , we could use Intervention Detection to find that point which provided the largest contrast between two local means. This would be referred to as a level shift or mean shift AND in general an intercept change . In that spirit I used AUTOBOX to analyze your first series. 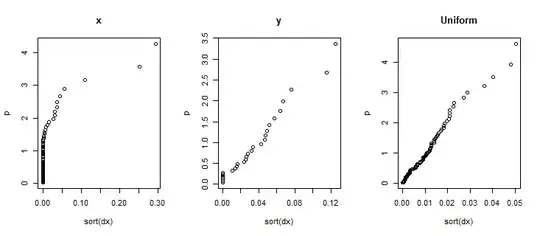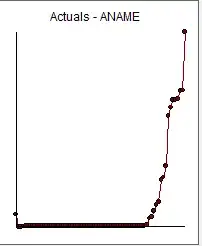Precisely I took your 72 values and ordered them from low to high and obtained the following which took into account non-constant error variance (visually obvious). Two tabular presentations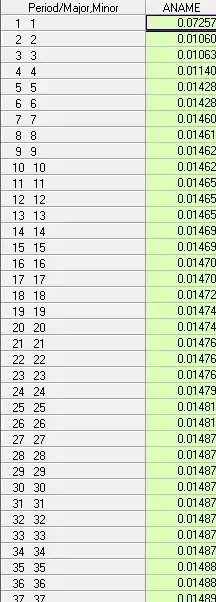

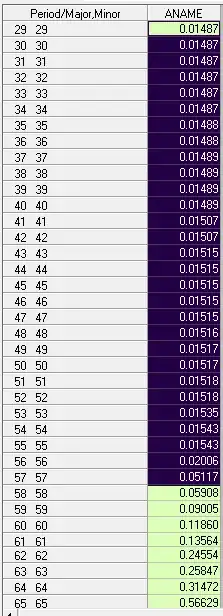
The equation that was automatically generated reflected memory as this was induced by the period-to-period auto-correlation in the series AND a suggestion that a level shift/break-point/intercept change was found at or around period 58 .. Looking at the second table the 58th value is .05908 . A more correct conclusion might have been point 57 .05117 but AUTOBOX for speed purposes does not evaluate each and every point in time. One could conclude that values from 0. to .02006 (the 56th value) were significantly different from the values from period 57 to 72. In this way one could then re-enter AUTOBOX with values 1-56 to identify possible sub-breaks AND values 57-73 to identify possible sub-breaks.In this iterative manner one might be able to solve your VERY thorny problem. The lack of any other response to your questions suggests that the resident experts have been baffled. Hope this helps.