1

How can I avoid my de-trending model from blowing up?

  • Do I need an additive model rather than a multiplicative model? If so, is there anything I would consequently need to take into account?
  • Can I simply identify series close to zero and add a constant?

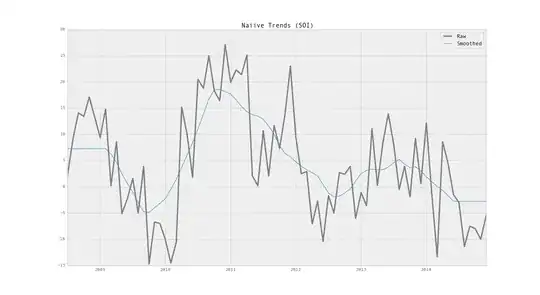
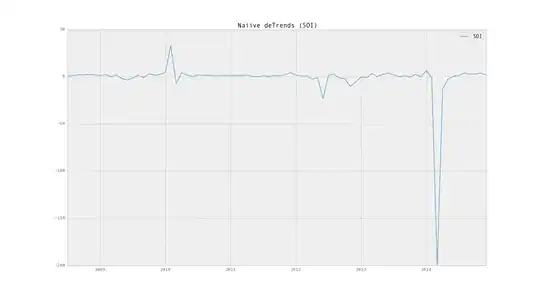
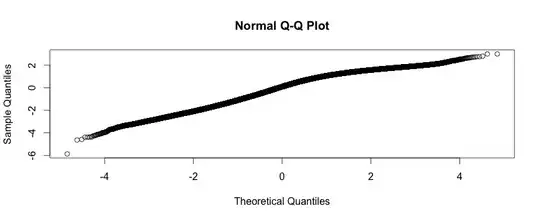
I have a series which moves about zero. Below is the series with an $S_{12\times 2}$ weighted moving average: enter image description here

The problem occurs when I divide the series by it's trend to de-trend the data. I get the following because the original dataset ~0 at February 2012: enter image description here

If I simply add 50 to the original series I get a decent result: enter image description here

Alexander McFarlane
  • 604
  • 1
  • 7
  • 17
  • It's strange to de-trend the series that *move about zero*. Doesn't this feature of your series imply that there is no trend? – Aksakal Jul 02 '15 at 14:36

2 Answers2

1

Subtracting, i.e. raw - smoothed, will avoid the divide by zero (near zero) that is "blowing up" your de-trending.

babelproofreader
  • 4,544
  • 4
  • 22
  • 35
1

I assume that you are trying to split the time series in the form:

y(t) = Trend(t) + Seasonality(t) + Random(t), given the measurements are taken after equal time intervals.

In general, the trend is a polynomial function of time. Therefore continuous differencing will detrend the series (but will create a completely different series). Eg: If the original series is I(1), then let z(t) = y(t+1) - y(t) for t = 1, 2, ..., n-1. If y has a linear trend, then z will be trendless. However, if y has higher order trend, then define p(t) = z(t+1) - z(t), q(t) = p(t+1) - p(t), ... till the final series becomes trendless. This process should be stopped when the first trendless series is obtained.

Presence of trend can be verified using Augmented Dickey-Fuller test. Use the following command in R: adf.test(column_vector) -> replace column_vector with z, p or q respectively.

Alternative:

You can use the command decompose in R. Given the seasonality, it will automatically split the time series into trend, seasonal and random components.

Caution:

Don't use log transformation unless the log(y2) - log(y1) makes sense. For example, in case of daily stock price data, log(y2) - log(y1) = Return on stock for 1 day.

Multiplicative Time Series:

Please refer this link

Another method:

You would be having the timestamps (t) associated with each observation. Remove the seasonal component and obtain another series x(t) = y(t) - Seasonality(t). Now regress x(t) with t and check for significance of coefficient of t. If it is significant with p-value < alpha, trend is a polynomial of order (at least) 1. Now add another column (t2) that is equal to square of the timestamp. Regress x(t) with t and t2 and check for significance of coefficient of t2. If it is significant, trend is a polynomial of order (at least) 2. Otherwise the trend is a polynomial of order = 1. Now add column t3, t4, ... till the order of the polynomial can be ascertained.

You can subtract beta1*t + beta2*t2 + ... + betan*tn from y(t) to detrend the series.

Community
  • 1
Naveen Mathew
  • 231
  • 1
  • 11
  • I was actually following the x11 process to compare results to the decompose function – Alexander McFarlane Jul 02 '15 at 20:28
  • Are you saying that I should incorporate differencing to remove all trends and then test for seasonality on the differences, skipping the de trending part – Alexander McFarlane Jul 02 '15 at 20:31
  • In my experience, seasonality is something that requires lot of effort to discover - must use as many dummy variables as the period. I assume that you already know the period. I'd suggest you to perform a seasonal difference instead of y2-y1, y3-y2, ... For example, if your seasonality is 12, make a new series z(t) = y(t+12) - y(t) for t=1,2,3, ... n-12. If the resulting series has a seasonality (maybe true if original series has 2 or more seasonal components), use seasonal differencing again. If it has trend only, use regular differencing: p(t) = z(t+1) - z(t), q(t) = p(t+1) - p(t), ... – Naveen Mathew Jul 03 '15 at 07:02