Simple voting scheme using confidence for each vote

Question

I am doing classification by splitting each observation into 14 subparts and then classifying each of these subparts individually. The overall classification of the observation is then performed using an ensemble of 14 votes.

I can see how much information is in each subpart (measured as # of interactions). I also know the relationship between the amount of information and the accuracy of classifying a subpart correctly. If the vote has been based on a low amount of information, the average accuracy is ~59%, whereas a high amount of information (100+ interactions in the plot below) will have a subpart classification accuracy of ~68%.

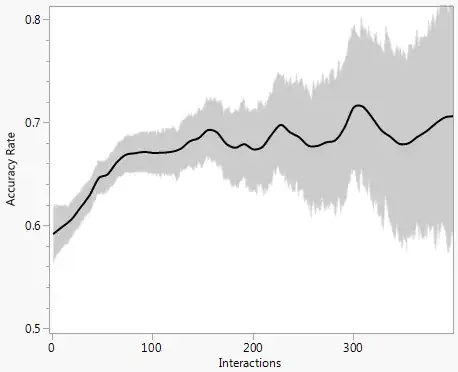
Currently I am simply averaging the votes to find the final result, but I would like to incorporate this knowledge into the voting scheme. How can I do that?

I have seen Voting system that uses accuracy of each voter and the associated uncertainty, but I am not interesting in a solution that involves solving a complex system or approximating a difficult to evaluate integral. Then I would rather use a simpler method that yields a slightly lower accuracy.

It should be noted that averaging the predictions give an accuracy of ~0.7 so the classifers are clearly not independent. That is also why it might even make sense to throw some votes away.

Edit: One important difference from many other voting schemes is that the confidence for the 14 votes for the subparts changes for each observation as some observations have a lot of information in subpart 1, while others will have a lot of information for subpart 14. Therefore, I cannot combine the voters using traditional meta-classification.

Answer 1

I see two ways how to deal with the situation like this. The very first approach is to use naive Bayesian classifier. In that case, you multiply the probabilities for yes and then for no and you normalize them. See this for details.

Another situation assumes that you have some annotated data, say $(x_i,y_i)$ where $x_i$ are inputs to the original classifiers and $y_i$ are the known categories. In that case, it is possible to consider a meta-classification. Let $z_{i,j}$ be result of the $j$-th sub-classifier applied to $i$-th data record, using $x_i$ input data. You can consider new classification problem $(z_i,y_i)$ where $z_i=(z_{i,1},z_{i,2},\dots,z_{i,n})$ where $n$ is number of sub-classifiers. In that case we can speak about some meta-classification.