25

If I understood correctly, in a machine learning algorithm, the model has to learn from its experience, i.e when the model gives the wrong prediction for the new cases, it must adapt to the new observations, and in time, the model becomes increasingly better. I don't see that the logistic regression has this characteristic. So why is it still regarded as a machine learning algorithm? What is the difference between logistic regression with the normal regression in term of "learning"?

I have the same question for random forests!

And what is the definition of "machine learning"?

Sycorax
  • 76,417
  • 20
  • 189
  • 313
Metariat
  • 2,376
  • 4
  • 21
  • 41
  • 4
    I edited your question for grammatical clarity, but am not sure what you mean overall... Logistic Regression falls under ML because it is a classification algorithm. Machine Learning does not imply that the algorithm has to be adaptive (although there are algorithms that learn from new observations). Adapting is more an implementation choice, usually achieved by generative machine learning algorithms which model the joint probability. – Zhubarb Jun 25 '15 at 13:06
  • 13
    "Machine learning" is a rather loosely defined concept. Really, all statistical procedures that involve fitting a model can be thought of machine learning. (Assuming the model fitting can be done by a computer, to some extent!). This is why some statistician get frustrated with "big data", "machine learning", etc communities muddying the waters about what statistics is (and isn't!) – P.Windridge Jun 25 '15 at 13:11
  • 1
    Related: [Are there algorithms for computing “running” linear or logistic regression parameters?](http://stats.stackexchange.com/q/23481/17230). – Scortchi - Reinstate Monica Jun 25 '15 at 13:32
  • 1
    @P.Windridge: if "all statistical procedures that involve fitting a model can be thought of machine learning" so I don't see why should we distinguish machine learning and statistic – Metariat Jun 25 '15 at 15:37
  • 4
    @XuanQuangDO We probably shouldn't distinguish machine learning and statistics. – Sycorax Aug 17 '15 at 12:36
  • Logistic regression is in no way a ML algorithm. Please see my answer below. – Antoine Aug 17 '15 at 14:22
  • @Zhubarb Logistic regression is not a classification algorithm. http://stats.stackexchange.com/questions/127042/why-isnt-logistic-regression-called-logistic-classification/127044#127044 – Sycorax Aug 26 '15 at 13:32
  • @user777, You can make your following statement for any classification algorithm that returns P(Ck|x) or P(Ck,x) : `It is only a classification algorithm in combination with a decision rule that makes dichotomous the predicted probabilities of the outcome` The exceptions are discriminant functions which directly return class memberships. Frank Harrell's argument against logistic regression being a classification algorithm is different from your quoted statement. – Zhubarb Aug 26 '15 at 14:32
  • @Zhubarb I don't understand how your comment refutes my position. Your first two sentences are consistent with my statement. – Sycorax Aug 26 '15 at 15:33

11 Answers11

25

Machine Learning is hot and is where the money is. People call things they're trying to sell whatever is hot at the moment and therefore "sells". That can be selling software. That can be selling themselves as current employees trying to get promoted, as prospective employees, as consultants, etc. That can be a manager trying to get budget approved from a company bigwig to hire people and buy stuff, or to convince investors to invest in his/her hot new startup which does Machine Learning as the key to making an improved sexting app. So software does Machine Learning and people are Machine Learning experts, because that's what's hot and therefore what sells ... at least for now.

I did all kinds of linear and nonlinear statistical model fitting more than 30 years ago. It wasn't called Machine Learning then. Now, most of it would be.

Just as everyone and their uncle is now a Data "Scientist". That's hot, that's supposedly sexy, so that's what people call themselves. And that's what hiring managers who have to get budget approved to hire someone list positions as. So someone who doesn't know the first thing about math, probability, statistics, optimization, or numerical/floating point computation, uses an R or Python package of dubious correctness and robustness of implementation, and which is labeled as a Machine Learning algorithm, to apply to data they don't understand, and call themselves a Data Scientist based on their experience in doing so.

This may sound flippant, but I believe it to be the essence of the situation.

Edit: The following was tweeted on September 26, 2019:

https://twitter.com/daniela_witten/status/1177294449702928384

Daniela Witten @daniela_witten "When we raise money it’s AI, when we hire it's machine learning, and when we do the work it's logistic regression."

(I'm not sure who came up with this but it's a gem )

Mark L. Stone
  • 12,546
  • 1
  • 31
  • 51
  • 18
    I won't hide that I share some of these opinions and am sympathetic to the rest. However, for them to be appropriate as an answer on an SE site they need to have some kind of support. Obviously that won't be through deductive reasoning: it has to come from adducing facts and/or citing authoritative sources. It would be cool if you could do that! – whuber Jun 25 '15 at 18:21
  • I could link to my own answer as the source. The OP asked a question which by its nature could, would, or should attract answers which are at least somewhat subjective. My answer falls into that category. If you don't think my answer is appropriate, then in my opinion you should think the question is not appropriate. I drew on my Economics background to help me come up with my answer. – Mark L. Stone Jun 25 '15 at 18:27
  • I should add, my answer could have mentioned universities trying to sell prospective students on admission by having machine learning majors, concentrations, courses, etc, and trying to sell enrolled students to take existing courses by relabeling them as machine learning or data science. Trying to sell deans, providers of research funds, etc. – Mark L. Stone Jun 25 '15 at 18:30
  • 11
    Easily the most entertaining post I've read today on this site, and I agree with much of it. But I have to agree with @whuber that it doesn't really answer the question in its current form. – Nick Cox Jun 25 '15 at 18:31
  • I disagree. I think it EXACTLY answers the OP's questions, even if it's not the traditional technical answer to a technical question which the editors are used to. My answer was meant to be complementary to the previous answers, so I didn't bother repeating those same answers. – Mark L. Stone Jun 25 '15 at 18:33
  • 3
    Re why not close the question: It boils down to the last line, "And what is the definition of "Machine Learning"?" That's a fair question which in principle can be answered dispassionately and objectively. (Whether it is easy to answer is another thing altogether. Nowhere on the website of the [Journal of Machine Learning](http://www.jmlr.org/) (formerly *Machine Learning*, dating back 14 years) can I find a definition. I cannot find one in Hastie & Tibshirani's highly respected *ESL*, either, although they repeatedly refer to "machine learning" as a discipline and a community.) – whuber Jun 25 '15 at 18:38
  • 1
    Have you noticed a big increase in things being called machine learning and people calling themselves machine learning experts in the last several years? That's just the "bubble" phenomenon, as with Dutch tulips, or the rare earths craze 4 years ago. Machine Learning has gotten past the knee in the curve, so now everyone is piling in and it's full speed ahead, until it collapses and people move on to the next hot thing. – Mark L. Stone Jun 25 '15 at 18:50
  • 2
    An "exact" answer [my lower case] would provide a definition as requested. I think you've provided a sharp and somewhat jaundiced commentary on what machine learning is often said to be. I can't see this as a definition. It's a personal rule of thumb that what distinguishes this forum from a set of intersecting blogs is an overriding concern for answering technical questions technically. That leaves plenty of scope for variations in personal style. – Nick Cox Jun 25 '15 at 18:50
  • 1
    This was a non-technical question, even if the OP didn't realize it at the time, and therefore in my opinion is deserving of a non-technical answer, even though it could be considered to be a technical answer in Economics - and that is exactly my point, the answer lies in Economics, not in "Cross Validation". But I do think whuber made a valuable contribution with the comment above on the journal and book not having definitions. – Mark L. Stone Jun 25 '15 at 18:53
  • 3
    I think it's important to try role reversal here. I am not a statistician but I regard myself as statistically minded. Naturally I hear lots of cutting comments about statistics: some are amusing, but few are really helpful to anyone. I think anyone who works under a heading of "machine learning" could feel the same way here about your post. (Let me stress again: I agree with much of it, but I don't think it quite fits here.) – Nick Cox Jun 25 '15 at 18:54
  • 2
    I won't delete my post, but feel free to delete it if you deem appropriate. – Mark L. Stone Jun 25 '15 at 18:56
  • 4
    As someone with the job title "Data Scientist" who humbly would like to believe that he does in fact know a few things about "math, probability, statistics, optimization, and numerical/floating point computation", and works with other like titled people who also know quite a lot about the same, what I'm left wondering is, where are these people that are getting hired but have none of these skills? What evidence do you have that you are not pointing fingers at unicorns? – Matthew Drury Jun 25 '15 at 19:04
  • 6
    As a small clarification. I work in both software development and the maligned "Data Science". I interview a lot of people. The rate of people interviewing for software development positions and data science positions who don't have the skills to do the job are about the same. So what's special about the data science title? People are going to inflate their skills in all technical disciplines. I'm sure programming stack exchange has many of the same complaints. – Matthew Drury Jun 25 '15 at 19:08
  • 1
    There is no doubt a large number of people, in absolute terms, who know what they're doing in and good at Machine Learning and Data Science, whatever they are :) . But especially in the last few years, there's a much larger number of people calling themselves Data Scientists who more closely match my earlier commentary. – Mark L. Stone Jun 25 '15 at 19:11
  • Maybe my bias is just to view that as the normal! – Matthew Drury Jun 25 '15 at 19:15
  • I wrote "So someone who doesn't know the first thing about math, probability, statistics, optimization, or numerical/floating point computation, ...", I did not write "everyone". – Mark L. Stone Jun 25 '15 at 19:17
  • Yah I know, I got carried away with the unicorn visual. I'm sorry about that. I just feel like it's about the same in all technical disciplines, so it's unfair to pick on data science. I should have said, instead of "where are they absolutely", "where are they relatively". – Matthew Drury Jun 25 '15 at 19:21
  • Yes, I remember when someone who knew how to format a floppy disk was a computer "expert". Someone who knew how to format a double density disk in a high density drive was a computer "scientist". – Mark L. Stone Jun 25 '15 at 19:21
  • 1
    @whuber I'm sure you know this, but for clarification I think it must be explicitly stated that *Journal of Machine Learning Research* is **not** the same as *Machine Learning*, as your comment implies. It's a different journal with a radically different vision, though it's about the same field and largely has the same editorial board (JMLR's board resigned at Machine Learning exactly because of vision). – Marc Claesen Jun 25 '15 at 21:03
  • 7
    This feels more like a rant than an answer. Sure, names change, branding is important and machine learning is hot (and hence has many self-proclaimed practitioners that don't know what they're doing). However, using that as an argument to downplay a field which has become established and highly relevant in both research and industry seems cheap to me. – Marc Claesen Jun 25 '15 at 21:12
  • 1
    I am not downplaying Machine Learning. I am not downplaying Data Science. I am downplaying the huge number of totally lame so-called practitioners of both and junky software and courses/books advertised as being machine learning or data science (tool), and junky work or products which are produced under those banners. – Mark L. Stone Jun 25 '15 at 21:46
  • 2
    Many of these Data Scientists are no more "scientists" than the person who knew how to execute a formatting command was a computer scientist. Such people and software (relatively numerous) devalue the truly good people and software (much less numerous). I'm considered to be an analyst, yet I am surrounded by "analysts" who are no more qualified to be an analyst than I am to be a brain surgeon. That diminishes my value as an analyst, because moderately astute managers recall the terrible analysis which has been performed by analysts, and therefore do not want to trust any analysts or analysis. – Mark L. Stone Jun 25 '15 at 21:51
  • 2
    I am laboring under the burden of knowing how to do statistical computing (learning from the first person to develop a practical algorithm to compute SVD), and knowing about numerical computing/numerical analysis in general, and nonlinear optimization in particular, and therefore realize just how bad a lot of the Python and R machine learning "solvers" really are, and how much better they could/should be. If your whole experience with computers was Windows ME, then you take it for granted that computers crash every hour or two. If your whole MLE experience is w/ R and Python MLE solvers, ... – Mark L. Stone Jun 25 '15 at 22:10
  • 2
    You may be right that the open source solvers are subpar, but it's hardly a burden to have the knowledge to improve them! You have the power to change the situation you are so frustrated with! – Matthew Drury Jun 25 '15 at 22:13
  • I'm not frustrated because I don't use them. I use good solvers, none of which say anything about being for MLE. Many VERY EXPENSIVE commercial products are totally lame, and are written by people who don't understand numerical; computing. On the other hand, some are good. – Mark L. Stone Jun 25 '15 at 22:16
  • 7
    @MarkL.Stone I understand your situation and I completely agree that there are many incompetent *insert hot term here*'s out there. However, in my opinion the fact such people find (and keep!) jobs is the fault of management. If managers are unhappy with the results of analysts, and treat all analysts the same regardless of individual skills/results, then the management is equally incompetent as the bad analysts. Any job that has a scent of cash has quacks, take medicine for instance. Sweeping generalizations about data scientists/machine learning guys are as bad as mistrusting all analysts. – Marc Claesen Jun 26 '15 at 06:42
  • 2
    @MarkL.Stone - So you're saying that all those open source R packages written by top scientists on the field (say, Breiman and Cutler's 'randomForest') are total rubbish? Interesting, but highly unlikely, especially for R. I do see a point in what you're trying to say but you fail to communicate it in your answer. Yes, there are many opportunists out there who claim to be experts in fields such as 'machine learning', 'data science', etc, but it has nothing to do with R, nor Python, nor the very real discipline of machine learning (which you did downplay). – Digio Sep 21 '15 at 15:12
  • 2
    If the usage of the term 'machine learning' has increased in the recent years it is also because the massive production of data has increased the needs of automated pattern recognition. As for the people who misuse those terms, there's a thing called 'job interview' that aims to expose them and, well, not hire them (trust me, it works every time). At the end of the day, I find that this conversation is irrelevant to this question and this website altogether. – Digio Sep 21 '15 at 15:13
  • @NickCox - From personal experience, I worked with a brilliant analyst who did not have a formal background in statistics (and didn't claim to be a statistician) but was a brilliant analyst & programmer (he was ranked #1 on Kaggle). I've also worked with people who edged sideways into statistics from other fields & perhaps padded their resume with sexy phrases like "predictive analytics". Whatever title an analyst uses, data scientist or statistician or machine learner, you don't *need* to have a degree in statistics to be a competent statistician (but it certainly doesn't hurt)! – RobertF Feb 08 '16 at 15:20
  • @NickCox - Having said that, part of the problem with the proliferation in titles & people with dubious qualifications claiming expertise is a lack of proper accreditation for statisticians (aside from a degree) in the United States, unlike other professional fields. – RobertF Feb 08 '16 at 15:42
24

Machine Learning is not a well defined term.

In fact, if you Google "Machine Learning Definition" the first two things you get are quite different.

From WhatIs.com,

Machine learning is a type of artificial intelligence (AI) that provides computers with the ability to learn without being explicitly programmed. Machine learning focuses on the development of computer programs that can teach themselves to grow and change when exposed to new data.

From Wikipedia,

Machine learning explores the construction and study of algorithms that can learn from and make predictions on data.

Logistic regression undoubtedly fits the Wikipedia definition and you could argue whether or not it fits the WhatIs defintion.

I personally define Machine Learning just as Wikipedia does and consider it a subset of statistics.

TrynnaDoStat
  • 7,414
  • 3
  • 23
  • 39
  • 1
    I agree with most of what you said, except that it is a subset of statistics. It has a large overlap, but there are types of learning, such as reinforcement learning, which can't really be considered to be a subset of statistics. – George Oct 16 '15 at 14:04
  • 2
    These are not good sources. – Neil G Nov 06 '15 at 12:29
  • @George Right, but let's face it, if you had to apply a label all data collection, analysis, and modeling methodologies, whether it's machine learning, supervised or unsupervised, parameteric or nonparametric, it's all statistics. ML is a specialized field in statistics. – RobertF Jun 29 '16 at 15:24
  • @RobertF I disagree. Machine learning is the field that studies how machines can learn. I agree that most methods used in ML can be considered statistical methods, but the field is not inherently a subfield of statistics. For example, I do not think Markov decision processes are considered statistical methods. – George Jul 03 '16 at 09:24
  • 1
    @George Discrete time Markov models are probability models. Once you estimate unknown parameters of a probability model (e.g. Markov decision processes) that is the textbook definition of a statistical procedure. I think the main class of activities that can be called ML and not statistics are specific applications, like building a robot that plays chess. The underlying algorithms will undoubtedly involve probability and statistics, but the application isn't really "statistics". Kind of like how genomics research uses statistics heavily, but they are decidedly different fields. – ahfoss Sep 03 '16 at 01:27
  • FWIW on Wikipedia it also says that in modern taxonomy, [phenetics](https://en.wikipedia.org/wiki/Phenetics) (classification based on characteristics) is mostly obsolete, and [phylogenetics](https://en.wikipedia.org/wiki/Phylogenetics) (classification based on descent) is dominant. Seems to depend on how much importance a taxonomist places on distinguishing inherited variations vs. convergent evolution. (Sorry, I could not resist, as this is a pet peeve for me: many people seem to think "common characteristics" is the only possible solution/use for taxonomy!) – GeoMatt22 Sep 20 '16 at 00:26
  • My impression of machine learning is that it is a subject that grew out of statistics but has now become more than a subset of statistics. Think of it this way; antibiotics were discovered by scientists but the person prescribing the antibiotics would be a doctor (not a biologist). A Data Scientists: better at statistics than a programmer & better at programming than a statistician. – josh Sep 22 '16 at 09:51
18

As others have mentioned already, there's no clear separation between statistics, machine learning, artificial intelligence and so on so take any definition with a grain of salt. Logistic regression is probably more often labeled as statistics rather than machine learning, while neural networks are typically labeled as machine learning (even though neural networks are often just a collection of logistic regression models).

In my opinion, machine learning studies methods that can somehow learn from data, typically by constructing a model in some shape or form. Logistic regression, like SVM, neural networks, random forests and many other techniques, does learn from data when constructing the model.

If I understood correctly, in a Machine Learning algorithm, the model has to learn from its experience

That is not really how machine learning is usually defined. Not all machine learning methods yield models which dynamically adapt to new data (this subfield is called online learning).

What is the difference between logistic regression with the normal regression in term of "learning"?

Many regression methods are also classified as machine learning (e.g. SVM).

Marc Claesen
  • 17,399
  • 1
  • 49
  • 70
  • 2
    Note that unsupervised learning is still called (machine) learning, so you don't necessarily need to have any feedback loop to classify something as "machine learning". – vsz Jun 26 '15 at 06:21
  • This isn't on topic for the question, but this answer mentions the separation between AI and ML as well. I always liked this definition of AI: https://en.wikipedia.org/wiki/AI_effect#AI_is_whatever_hasn.27t_been_done_yet – Davis Yoshida Jul 17 '15 at 01:24
12

Logistic regression was invented by statistician DR Cox in 1958 and so predates the field of machine learning. Logistic regression is not a classification method, thank goodness. It is a direct probability model.

If you think that an algorithm has to have two phases (initial guess, then "correct" the prediction "errors") consider this: Logistic regression gets it right the first time. That is, in the space of additive (in the logit) models. Logistic regression is a direct competitor of many machine learning methods and outperforms many of them when predictors mainly act additively (or when subject matter knowledge correctly pre-specifies interactions). Some call logistic regression a type of machine learning but most would not. You could call some machine learning methods (neural networks are examples) statistical models.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
  • 1
    Funnily Amazon's *machine learning* service uses only one algorithm (afaik) - *logistic regression* - for *classification* tasks :p https://aws.amazon.com/machine-learning/faqs/ – stmax Aug 27 '15 at 10:08
  • You could just present the data incrementally — as in an *online learning problem*. In that case, logistic regression doesn't "get it right the first time". I progressively learns. It has a standard loss, and its update is standard application of gradient descent. Logistic regression is in every machine learning text book that I've seen. – Neil G Nov 06 '15 at 12:34
  • 1
    The fact that you could sample data in an incremental fashion can apply to any estimator even a mean so keep that separate. In a method such as logistic models where the first and second derivatives of the log likelihood function are available analytically you just use the ultra-fast Newton-Raphson method with step-halving to estimate $\beta$ with initial estimates set to zero except for the intercept. – Frank Harrell Nov 06 '15 at 13:50
  • @FrankHarrell: Right, and that's how maximum likelihood estimation of the solution of a logistic regression problem proceeds. – Neil G Nov 06 '15 at 17:18
  • Logistic regression may predate the **term** "Machine Learning", but it doesn't predate the **field**: SNARC was developed in 1951 and was a **learning machine**. Also, the insistence that logistic regression only models probabilities, and is not, by itself, a classifier, is hair-splitting. By that logic, a neural network is not a classifier (unless the output layer consists of binary neurons, but that would make backpropagation impossible). – Igor F. Dec 19 '19 at 11:47
8

I'll have to disagree with most of the answers here and claim that Machine Learning has a very precise scope and a clear cut distinction from Statistics. ML is a sub-field of computer science with a long history, which only in recent years has found applications outside its domain. ML's paternal field and application domain lies within Artificial Intelligence (robotics, pattern recognition software, etc), therefore, it's not just a "hot term" like "Big Data" or "Data Science". Statistics, on the other hand, (which comes from the word "state") was developed within social and economical sciences as a tool for humans, not machines. ML evolved separately from statistics and, eventhough somewhere along the way it started relying heavily on statistical principles, it is by no means a subfield of statistics. ML and statistics are complementary, not overlapping fields.

Long answer:

As implied by its name ML methods were made for software/machines while statistical methods were made for humans. Both ML and statistics deal with predictions on data, however, ML methods follow a non-parametric automatised approach whereas statistical methods require a great deal of manual model-building work with an added explanatory factor. This makes perfect sense if you consider that ML algorithms were developed in AI research as a means of automatised prediction-making that was meant to be integrated in robotics software (e.g. for the purposes of voice and face recognition). When a "machine" makes a prediction, it doesn't care about the reasons behind it. A machine doesn't care to know the drivers/predictors behind a model which classifies email as spam or non-spam, it only cares to have the best accuracy of prediction. This is why virtually all ML methods are black boxes, it's not because they don't have a model, it's because the model is constructed algorithmically and not meant to be visible to neither human nor machine.

The concept of "training" in ML relies on computational power, whereas statistical model-building with OLS-type of methods for parameter estimation relies on the knowledge of a human expert. In a multiple regression scenario it's strictly up to the statistician to use his expert judgement in order to choose his model and verify all required statistical assumptions. A statistician's goal is not just to find patterns and use them for predictions but also to understand his data and his problem in a much greater depth than ML.

Of course in some occasions ML and statistics do overlap, as is the case with many disciplines. Logistic regression is one of these occasions; originally a statistical method, which bears so much resemblance to the simple Perceptron (one of the most fundamental ML techniques), that it is by some seen as a ML method.

Digio
  • 2,427
  • 12
  • 18
  • 1
    Perhaps you've never heard of nonparametric statistics and nonparametric statistical models and model building? – Mark L. Stone Jul 25 '15 at 15:12
  • 1
    Yes, I use nonparametric stats on a daily basis. I didn't say that ML is the nonparametric answer to statistics, I just find that ML methods being nonparametric comes as a side-effect. Nonparametric statistics is an alternative option of the statistician when parametric statistics fails, but it's still the result of an expert's conscious choice. I'm probably not being clear enough in communicating my view and for that I apologise. – Digio Jul 25 '15 at 21:21
  • 3
    There are plenty of statisticians who do nonparametric models, statistics all the time. Have you heard of Empirical Likelihood - invented by a statistician, used by statisticians, and quite nonparametric, although it can also be used in a semi-parametric fashion. So I disagree with you, but I did not downvote you. – Mark L. Stone Jul 25 '15 at 22:39
  • 1
    Disagreeing is fine Mark but I still don't quite understand what your counter argument is about. Are you implying that nonparametric statistics has no need of machine learning (something I never denied)? Or are you claiming that machine learning is in fact just another name for nonparametric statistics (something I did deny)? – Digio Jul 26 '15 at 07:07
  • You seem to be saying or strongly suggesting that nonparametric methods are what distinguish distinguish machine learning from statistics. I disagree with that. if you are not trying to say that, perhaps you should clarify your post. – Mark L. Stone Jul 26 '15 at 14:01
  • 1
    Yes, ML methods are generally nonparametric (maybe with few exceptions) but I'm not suggesting that machine learning is an alternative name for nonparametric statistics. I'm suggesting that ML methods for prediction and statistical methods for prediction (parametric or not) evolved separately from each other and met in the middle. Artificial neural networks, k-nearest neighbours, support vector machine, decision trees, these are some typical examples of machine learning algorithms that were invented within Artificial Intelligence and computational learning theory, not within statistics. – Digio Jul 26 '15 at 16:58
  • 1
    [continued]... Does statistics have nonparametric methods of its own that perform the same tasks? Yes, but it doesn't mean that machine learning and statistics are the same discipline like many people suggest. I expect to get downvoted by statisticians (ironically I'm one as well) but that's OK. – Digio Jul 26 '15 at 17:00
  • 3
    There is much to disagree with here. Multivariable regression models, when used in conjunction with modern statistical tools, can be flexible and highly competitive with ML. – Frank Harrell Aug 17 '15 at 12:55
3

Machine learning is pretty loosely defined and you're correct in thinking that regression models--and not just logistic regression ones--also "learn" from the data. I'm not really sure if this means machine learning is really statistics or statistics is really machine learning--or if any of this matters at all.

However, I don't think it's necessary for an algorithm to repeatedly learn from its mistakes. Most methods use a training set to calculate some parameters and then use these fixed parameters to make predictions on some additional test data. The training process may involve repeatedly updating the parameters (as in backpropagation), but it doesn't necessarily ($k$-nearest neighbours doesn't do anything at all during training!). In any case, at test-time, you may not even have access to ground-truth data.

That said, some algorithms do learn from prediction errors--this is particularly common in reinforcement learning, where an agent takes some action, observes its result, and then uses the outcome to plan future actions. For example, a robotic vacuum might start with a model of the world where it cleans all locations equally often, and then learn to vacuum dirty places (where it is "rewarded" by finding dirt) more and clean places less.

Online or incremental algorithms can be repeatedly updated with new training data. This doesn't necessarily depend on the model's prediction accuracy, but I could imagine an algorithm where the weights are updated more aggressively if, for example, the new data seems very unlikely given the current model. There are online versions for logistic regression: e.g., McMahan and Streeeter (2012).

Matt Krause
  • 19,089
  • 3
  • 60
  • 101
3

I finally figured it out. I now know the difference between statistical model fitting and machine learning.

  • If you fit a model (regression), that's statistical model fitting
  • If you learn a model (regression), that's machine learning

So if you learn a logistic regression, that is a machine learning algorithm.

Comment: Pardon me for being an old geezer, but whenever I hear people talking about learning a model, or learning a regression, it makes me think of Jethro "I done learned me an education".

END OF THREAD

Mark L. Stone
  • 12,546
  • 1
  • 31
  • 51
  • ??? I can also learn a logistics model, what're you talking about? – SmallChess Dec 23 '15 at 08:44
  • 1
    @Student T , if you fit a logistics model, that is statistical model fitting. If you learn a logistics model, that is machine learning.I.e., it's really a matter of the terminology used by the different fields. The same thing can be called different things by different fields (Statistics and Machine Learning). – Mark L. Stone Dec 23 '15 at 12:57
0

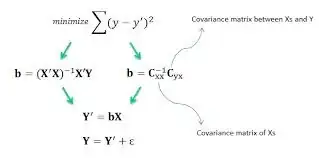
Logistic regression (and more generally, GLM) does NOT belong to Machine Learning! Rather, these methods belongs to parametric modeling.

Both parametric and algorithmic (ML) models use the data, but in different ways. Algorithmic models learn from the data how predictors map to the predictand, but they do not make any assumption about the process that has generated the observations (nor any other assumption, actually). They consider that the underlying relationships between input and output variables are complex and unknown, and thus, adopt a data driven approach to understand what's going on, rather than imposing a formal equation.

On the other hand, parametric models are prescribed a priori based on some knowledge of the process studied, use the data to estimate their parameters, and make a lot of unrealistic assumptions that rarely hold in practice (such as the independence, equal variance, and Normal distribution of the errors).

Also, parametric models (like logistic regression) are global models. They cannot capture local patterns in the data (unlike ML methods that use trees as their base models, for instance RF or Boosted Trees). See this paper page 5. As a remediation strategy, local (i.e., nonparametric) GLM can be used (see for instance the locfit R package).

Often, when little knowledge about the underlying phenomenon is available, it is better to adopt a data-driven approach and to use algorithmic modeling. For instance, if you use logistic regression in a case where the interplay between input and output variables is not linear, your model will be clearly inadequate and a lot of signal will not be captured. However, when the process is well understood, parametric models have the advantage of providing a formal equation to summarize everything, which is powerful from a theoretical standpoint.

For a more detailed discussion, read this excellent paper by Leo Breiman.

Antoine
  • 5,740
  • 7
  • 29
  • 53
  • 4
    Please take the time to understand logistic regression. It makes no distributional assumptions whatsoever. It makes exactly the same kind of independence assumption made by ML. ML requires much larger sample sizes than logistic regression. For example, random forests and SVM can require 200 events per candidate feature to be stable whereas logistic regression typically requires 200 events per candidate variable. – Frank Harrell Aug 17 '15 at 12:52
  • 2
    *You* should take the time to understand logistic regression! It is a Generalized **Linear** Model where the link is the logit function. It is parametric. It assumes that the observations are IID. Also, good luck with capturing nonlinear relationships. Also, what does the second portion of your sentence mean? To me, a feature is a variable (?) – Antoine Aug 17 '15 at 13:30
  • 5
    There are plenty of good books on the subject and I recommend you consult them before proceeding. Logistic regression does not assume identical distributions and in effect assumes no distribution at all. Unless you can demonstrate how you factor in correlation structure in ML, both approaches assume independence. Regression splines have been used since 1982 to relax linearity assumptions in logistic regression. For this discussion feature=variable unless expanded in a spline. – Frank Harrell Aug 17 '15 at 14:42
  • 1
    Speaking of good references, why don't you take a look at the [paper](http://projecteuclid.org/download/pdf_1/euclid.ss/1009213726) I cited in my answer? I explains in detail the serious limitations suffered by logistic regression, and why logistic regression radically differs from ML. It also shows that ML can be 30% more accurate than logistic regression is some cases. But maybe [Leo Breiman](https://en.wikipedia.org/wiki/Leo_Breiman) should also have taken the time to understand logistic regression? – Antoine Aug 18 '15 at 09:40
  • 5
    Breiman understood things quite well. He just didn't deal with post 1982 developments in logistic regression, e.g. penalized maximum likelihood estimation, regression splines, and combinations with data reduction methods. The only serious limitation to logistic regression is that like other methods it is not good at finding the right interactions if one searches for interactions and they are not pre-specified. Most methods that purport to be able to do this do not result in replicable findings. Also, Breiman used an improper accuracy score that can be optimzed by a bogus model. – Frank Harrell Aug 18 '15 at 12:19
  • 3
    @Antoine: "why logistic regression radically differs from ML". Notice that some methods in ML (most noticeably, SVM) are very much related to logistic regression. With the exception of multiple interactions -as Frank wrote- logistic reg with non-linearities and penalization give very similar results to SVM and other ML methods. It continues to amaze me how some papers cite performance improvements based of an ML method vs. a stat101 logistic model to negatively frame logistic regression. – Thomas Speidel Aug 18 '15 at 14:25
  • 1
    @FrankHarrell Would you happen to have citation handy for this remark? I'd be interested in learning more about this topic! "ML requires much larger sample sizes than logistic regression. For example, random forests and SVM can require 200 events per candidate feature to be stable whereas logistic regression typically requires 200 events per candidate variable." – Sycorax Aug 26 '15 at 13:30
  • Logistic regression is typically 15-20 per variable. See http://www.citeulike.org/user/harrelfe/article/13467382 – Frank Harrell Aug 26 '15 at 22:08
  • 2
    @FrankHarrell: You're wrong that logistic regression doesn't make distributional assumptions. Logistic regression is equivalent to an assumption that the target is Bernoulli distributed. – Neil G Nov 06 '15 at 12:32
  • Please let me know which realizations of binary events that are independent causes distributional problems for the logistic model. The Bernoulli distriibution is very hard to not fit. – Frank Harrell Nov 06 '15 at 13:57
  • 1
    @FrankHarrell: The point is that fitting logistic regression is the same problem as fitting a model whose target is Bernoulli-distributed with unknown bias $p$ (and some other independence assumptions). See my answer here for the connection between the Bernoulli distribution and logistic regression: http://stats.stackexchange.com/questions/145272/how-is-softmax-unit-derived-and-what-is-the-implication/145277#145277 – Neil G Nov 06 '15 at 17:24
  • Give me an example where there are two possible outcomes, the same two potential outcomes for each subject, the outcomes are independent, and the univariate distribution is not Bernoulli. – Frank Harrell Nov 07 '15 at 14:07
  • 2
    @FrankHarrell FYI when you reply to someone here please use @ otherwise, no one gets notified. Also I have no idea what your question has to do with your earlier claim that logistic regression makes no distributional assumptions. (And just to be clear "the outcomes are independent" doesn't make any sense — events can be dependent; not outcomes.) – Neil G Nov 07 '15 at 17:34
  • @NeilG I see that you were unable to meet my challenge. Events and outcomes are interchangeable here. Two binary random variables Y1 and Y2 having potential outcomes 0 and 1 are independent if and only if Prob(Y1=y1, Y2=y2) = Prob(Y1=y1)Prob(Y2=y2). But the original issue is my statement that the binary logistic regression model makes no distributional assumptions where I'm implying no distributional assumptions that have any likelihood of not being satisfied. Your other posting to which you linked above has an incorrect conclusion regarding sufficient statistics, which need not exist. – Frank Harrell Nov 08 '15 at 13:32
  • @FrankHarrell: Events and outcomes are not interchangeable, but it looks like what you're saying is that the target realizations are independent **given the inputs** (you do need to add that to your equation — without that, your model could not learn anything except a bias!) Like I explained in my link, the logistic model makes a Bernoulli assumption. You say "no distributional assumptions that have any likelihood of not being satisfied", but there are plenty of other models that output a number on a closed interval like $[0, 1]$ and do not make this distributional assumption, for example: – Neil G Nov 10 '15 at 03:22
  • 1
    (1) truncated linear regression, which corresponds to a truncated Gaussian model, (2) regression using the sufficient statistics of the von Mises von-Mises distribution, (3) truncated exponential regression, etc. Also, if you have comments about how my linked answer "has an incorrect conclusion" please share it in the comments below it so that we may all benefit from your experience. – Neil G Nov 10 '15 at 03:24
  • 1
    First, it is not necessary for sufficient statistics to exist for a model to be a valid model (this related to your other post). Second, you still have not provided an example of a binary random variable with independent events/outcomes and the same 2 outcome possibilities for every observation where the distribution is not Bernoulli. Third, binary outcomes can be independent unconditionally on the inputs as well as conditionally. Having independent variables relating to $Y$ just makes the Bernoulli random variates not identically distributed, i.e., have varying probabilities that $Y=1$. – Frank Harrell Nov 10 '15 at 03:50
  • 1
    @FrankHarrell Going back to your statement, you said that logistic regression makes no distributional assumptions. I think we agree that it minimizes the surprise of a Bernoulli random variable. And yes I agree that there are no other two-outcome models having "conditionally independent realizations" ("independent outcomes" is nonsense). However, logistic regression does make a distributional assumption compared to other models whose output is real-valued over an interval; the outputs of these other models need not be interpreted as the unknown bias of a Bernoulli variable. – Neil G Nov 10 '15 at 04:15
  • 2
    You are confusing distributional assumptions (left hand side of a regression model) with link function and regression assumptions (right hand side of the model). You can use a huge variety of link functions providing the underlying heterogeneous probabilities for a Bernoulli sequence (see the original paper on the logistic model - Cox, 1958). That in no way changes that it is a Bernoulli sequence. And your disagreement over 'outcomes' must stem from my lack of specificity of 'outcomes' vs. 'potential outcomes'. Using new terms for old things, e.g. "surprise" vs. likelihood is suboptimal. – Frank Harrell Nov 10 '15 at 12:22
  • P.S. For example, probit binary regression using the Gaussian cumulative distribution function to translate the linear predictor $X\beta$ into probabilities. *Nowhere* in the probit model is a normal distribution assumed for anything. – Frank Harrell Nov 10 '15 at 16:05
  • @FrankHarrell: *Outcome* is a technical term, which is any member of the sample space. That's why there is no such thing as "independent outcomes". You can look in the introduction of any statistics textbook for that. *Surprisal* is also a technical term, which is the negative log likelihood. Minimizing the surprisal is the same as maximizing the likelihood. It is more convenient mathematically to minimize the surprisal. – Neil G Nov 10 '15 at 18:32
  • You started out by saying that there were no distributional assumptions. Then you said that there were distributional assumptions, but not any "that had any likelihood of not being satisfied". Now you're back to saying there are no distributional assumptions. Make up your mind. Are there distributional assumptions or not? Thinking of link functions without their distributional assumptions is just burying your head in the sand. Since the loss function is the same as if you had made a particular set of distributional assumptions, then you are making them whether you like it or not. – Neil G Nov 10 '15 at 18:38
  • 2
    I see that you remain unable to meet my challenge. There seem to be no distributional assumptions that you have been able to invalidate. The Bernoulli distribution on $Y=0,1$ is "always there". So you may choose to call that an assumption. I choose to not worry about assumptions that are always satisfied. Your misunderstanding is typified by "link functions without their distributional assumptions." Link functions do not pertain to distributions; they pertain to the mathematical relationship between $X\beta$ and a statistical property of the response $Y$ such as $E(Y)$ or $Prob(Y=1)$. – Frank Harrell Nov 10 '15 at 19:06
  • @FrankHarrell: If "[l]ogistic regression [...] in effect assumes no distribution at all", how does logistic function, as the modeled probability, come into being? Why logistic, and not any other of the myriad monotonous functions bounded to (0 ,1) (e.g. $arc tan(x)$ or $erf(x)$ with a proper scaling)? – Igor F. Dec 19 '19 at 11:31
-1

I think the other answers do a good job at identifying more or less what Machine Learning is (as they indicate, it can be a fuzzy thing). I will add that Logistic Regression (and its more general multinomial version) is very commonly used as a means of performing classification in artificial neural networks (which I think are unambiguously covered by whatever sensible machine learning definition you choose), and so if you mention Logistic Regression to a neural net person, they are likely to immediately think of it in this context. Getting tied up with a heavy hitter in machine learning is a good way to become a machine learning technique yourself, and I think to some extent that is what happened with various regression techniques, though I wouldn't discount them from being proper machine learning techniques in and of themselves.

adamconkey
  • 561
  • 4
  • 11
  • Note that logistic regression is not a classifier but a direct probability estimation method. – Frank Harrell Aug 18 '15 at 12:20
  • For further information on Dr. Harrell's point, please see my post here. http://stats.stackexchange.com/questions/127042/why-isnt-logistic-regression-called-logistic-classification/127044#127044 – Sycorax Aug 26 '15 at 13:21
  • @FrankHarrell We can also use the probability for classification, so it's really a classifier. – SmallChess Dec 23 '15 at 08:45
  • @StudentT4 That could not be more incorrect. If is a direct probability estimator. How you use the final result of the logistic model is up to you. By your logic the sample mean is a classifier. – Frank Harrell Dec 23 '15 at 13:39
-1

I think any procedure which is "iterative" can be considered a case of machine learning. Regression can be considered machine learning. We could do it by hand, but it would take a long time, if at all possible. So now we have these programs, machines, which do the iterations for us. It gets closer and closer to a solution, or to the best solution or best fit. Thus, "machine learning". Of course things like neural networks get most of the attention in regard to machine learning, so we usually associate machine learning to these sexy procedures. Also, the difference between "supervised" and "unsupervised" machine learning is relevant here

dailyl
  • 1
  • 2
-2

It is a very common mistake that most people do and i can see it here also (done by almost everyone). Let me explain it in detail... Logistic Regression and linear Regression model, both are parametric model as well as Machine Learning Technique. It just depends on the method you are using to estimate the model parameters(theta's). There are 2 ways of finding model parameters in Linear Regression and Logistic reg.

  1. Gradient Descent Technique: Here we starts by assigning random values to the parameters and find cost function(error). In each iteration we update our parameters and minimize cost function. After certain number of iterations, cost function reduced to desired values and corresponding parameters values are our final values. This is what a machine learning techniques supposed to do. So, if You are using Gradient Descent technique, Logistic regression can call as a machine learning technique.

  2. By using Least Square Method: Here we have direct formula to find our parameters (some matrix algebra is required to understand the derivation of this formula) which is known as normal equation. Least Square Method

Here b represents parameters X is design Matrix. Both Methods have their own advantages and limitations. To get more details: follow coursera Machine Learning course still running.

I hope this post might be helpful .. :-)

Mohit Kumar
  • 11
  • 2