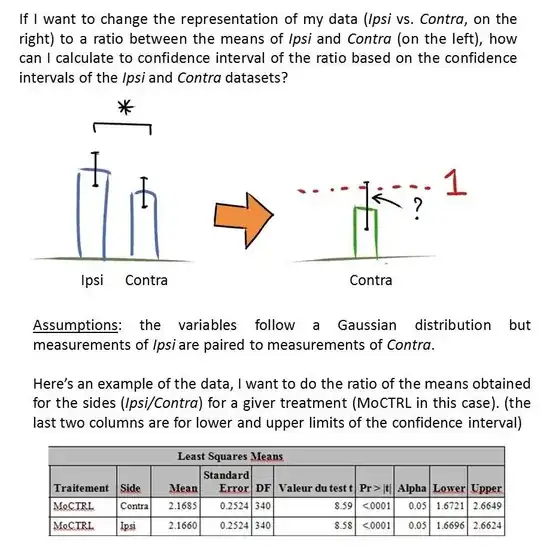
If you have two means (with their own confidence intervals) and want to represent them as a ratio, how do calculate the confidence interval for the ratio?
An answer that was given to me, mentions Fieller's theorem, which enables you to compute a confidence interval for a ratio quite easily (see calculator here).
Unfortunately, I cannot use this tool as my measurements are paired. Is there any way around this?