I am trying to understand the interpretation of radial basis functions (RBFs) as networks and then trying to understand the relationship it has to "normal" neural networks and how to extend them to multiple layers.
For this I was watching the lectures from the caltech course CS156 and they present the following slide:
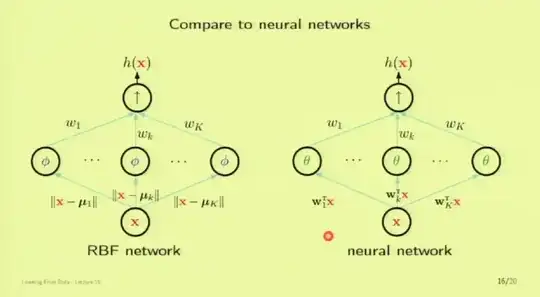
This slide shows that RBF networks and neural networks are quite different and extending the RBF network to multiple laters is not 100% clear to me how it would be done (or if it even makes sense to do).
One way that I thought to extend RBFs to multiple layers is by having a general neural network as a usual neural network, but then substitute each activation function with a Gaussian function.
However, I thought of a different way of doing it more similar to the way the RBF network is build but extend that recursively. The main idea is to make sure each later computes feature based on the distance to a center with respect to the previous layer. Something of the form:
$$ x^{(l)}_k = \phi( \| x^{(l-1)} - \mu^{l}_k \| )$$
where $x^{(l)}_k$ denotes the output of the activation of a certain activation node in the neural network. The idea is that its getting the whole output of the previous later, computing a distance with respect to a center of the current hidden layer and then applying an non-linearity to it. To illustrate my idea, here how the first later would look:
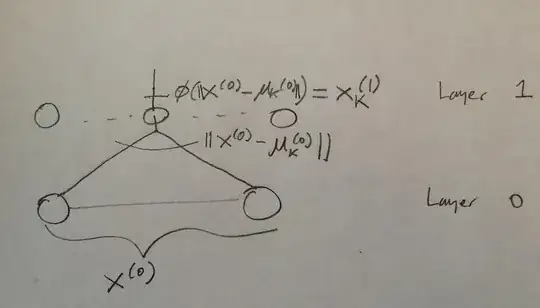
For a arbitrary layer:
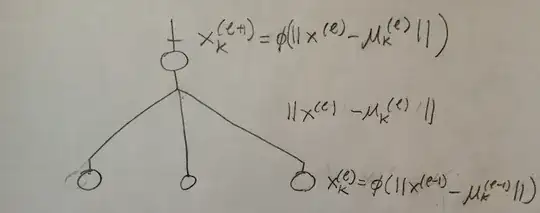
The issue with such a network is that even though it makes sense as a generalization to the RBF netowrk, its structure is completely different from neural networks since only the last layer has weights to be updated. Another issue is choosing the centers. The centers could just be chosen with k-means at each layer but I am not 100% if this is justifiable in any framework (like regularization).
Anyway, my main question is, how are RBF networks extended to use multiple lyaers like the multiple layer perceptron (MLP/neural networks) are used. I provided two suggestion but wasn't sure which was correct or which one was actually used or which one actually had some research done.