Can a neural network learn a functional, and its functional derivative?

Question

I understand that neural networks (NNs) can be considered universal approximators to both functions and their derivatives, under certain assumptions (on both the network and the function to approximate). In fact, I have done a number of tests on simple, yet non-trivial functions (e.g., polynomials), and it seems that I can indeed approximate them and their first derivatives well (an example is shown below).

What is not clear to me, however, is whether the theorems that lead to the above extend (or perhaps could be extended) to functionals and their functional derivatives. Consider, for example, the functional: \begin{equation} F[f(x)] = \int_a^b dx ~ f(x) g(x) \end{equation} with the functional derivative: \begin{equation} \frac{\delta F[f(x)]}{\delta f(x)} = g(x) \end{equation} where $f(x)$ depends entirely, and non-trivially, on $g(x)$. Can a NN learn the above mapping and its functional derivative? More specifically, if one discretizes the domain $x$ over $[a,b]$ and provides $f(x)$ (at the discretized points) as input and $F[f(x)]$ as output, can a NN learn this mapping correctly (at least theoretically)? If so, can it also learn the mapping's functional derivative?

I have done a number of tests, and it seems that a NN may indeed learn the mapping $F[f(x)]$, to some extent. However, while the accuracy of this mapping is OK, it is not great; and troubling is that the computed functional derivative is complete garbage (though both of these could be related to issues with training, etc.). An example is shown below.

If a NN is not suitable for learning a functional and its functional derivative, is there another machine learning method that is?

Examples:

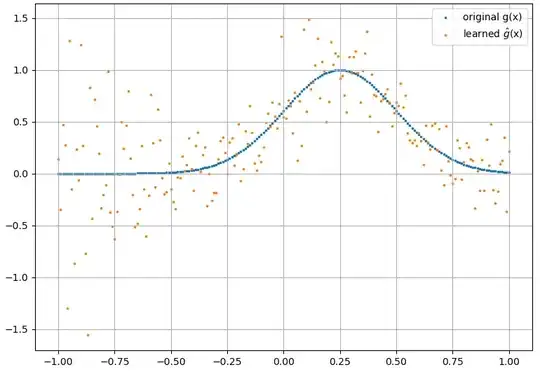
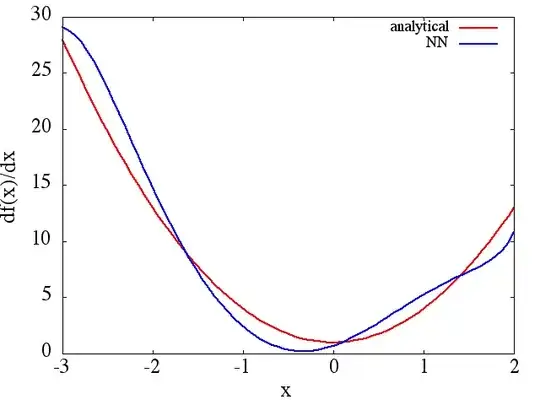
(1) The following is an example of approximating a function and its derivative: A NN was trained to learn the function $f(x) = x^3 + x + 0.5$ over the range [-3,2]: from which a reasonable approximation to $df(x)/dx$ is obtained: Note that, as expected, the NN approximation to $f(x)$ and its first derivative improve with the number of training points, NN architecture, as better minima are found during training, etc.

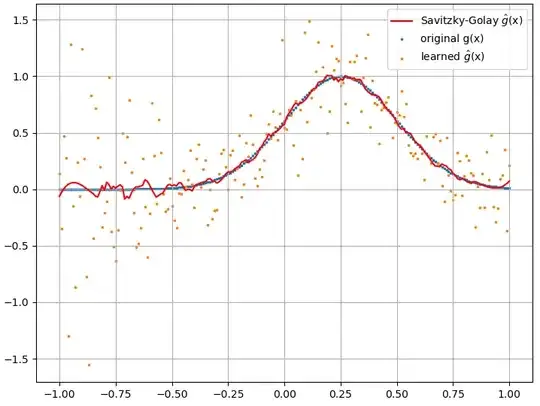
(2) The following is an example of approximating a functional and its functional derivative: A NN was trained to learn the functional $F[f(x)] = \int_1^2 dx ~ f(x)^2$. Training data was obtained using functions of the form $f(x) = a x^b$, where $a$ and $b$ were randomly generated. The following plot illustrates that the NN is indeed able to approximate $F[f(x)]$ quite well: 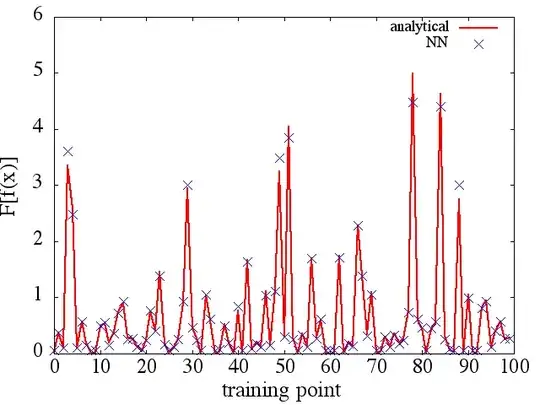Calculated functional derivatives, however, are complete garbage; an example (for a specific $f(x)$) is shown below: 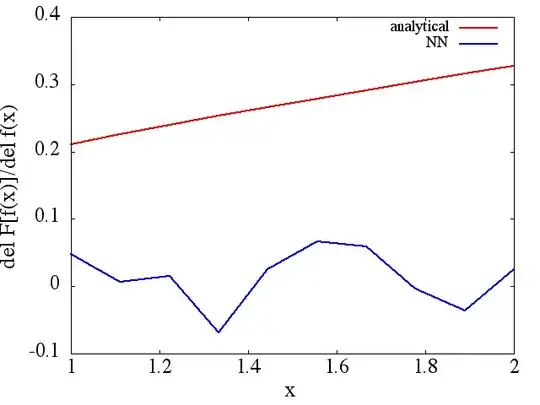As an interesting note, the NN approximation to $F[f(x)]$ seems to improve with the number of training points, etc. (as in example (1)), yet the functional derivative does not.

Answer 1

This is a good question. I think it involve theoretical mathematical proof. I have been working with Deep Learning (basically neural network) for a while (about a year), and based on my knowledge from all the papers I read, I have not seen proof about this yet. However, in term of experimental proof, I think I can provide a feedback.

Let's consider this example below:

In this example, I believe via multi-layer neural network, it should be able to learn both f(x) and also F[f(x)] via back-propagation. However, whether this apply to more complicated functions, or all functions in the universe, it require more proofs. However, when we consider the example of Imagenet competition --- to classify 1000 objects, a very deep neural network are often used; the best model can achieve an incredible error rate to ~5%. Such deep NN contains more than 10 non-linear layers and this is an experimental proof that complicated relationship can be represented through deep network [based on the fact that we know a NN with 1 hidden layer can separate data non-linearly].

But whether ALL derivatives can be learned required more research.

I am not sure if there any machine learning methods that can learn the function and its derivative completely. Sorry about that.

Answer 2

Neural nets can approximate continuous mappings between Euclidean vector spaces $f : \mathbb{R}^M \to \mathbb{R}^N$ when the hidden layer becomes infinite in size. That said, it's more efficient to add depth than width. A functional is simply a map where the range is $\mathbb{R}$ i.e. $N=1$. So yes, neural nets can learn functionals as long as the input is a finite dimensional vector space and the derivative is easily found by reverse-mode differentiation aka backpropagation. Also, quantising the input is indeed a good way to extend the network to continous function inputs.

Answer 3

If the functional is in the form $$F[f(x)]=\int\limits_a^bf(x)g(x)dx$$ then $g(x)$ can be learned with a linear regression given enough training functions $f_i(x), ~i=0,\dots,M$ and target values $F[f_i(x)]$. This is done approximating the integral by a trapezoidal rule: $$F[f(x)]= \Delta x\left[\frac{f_0g_0}{2}+f_1g_1+...+f_{N-1}g_{N-1}+\frac{f_Ng_N}{2}\right]$$ that is $$\frac{F[f(x)]}{\Delta x}=y= \frac{f_0g_0}{2}+f_1g_1+...+f_{N-1}g_{N-1}+\frac{f_Ng_N}{2}$$ where $$f_0=a,~f_1=f(x_1),~...,~f_{N-1}=f(x_{N-1}),~f_N=b,$$ $$a<x_1<...<x_{N-1}<b,~~\Delta x=x_{j+1}-x_j$$

Suppose we have $M$ training functions $f_i(x),~i=1,\dots,M$. For each $i$ we have $$\frac{F[f_i(x)]}{\Delta x}=y_i= \frac{f_{i0}g_0}{2}+f_{i1}g_1+...+f_{i,N-1}g_{N-1}+\frac{f_{iN}g_N}{2}$$

The values $g_0,\dots, g_N$ are then found as a solution of a linear regression problem with a matrix of explanatory variables $$X=\begin{bmatrix} f_{00}/2 & f_{01} & \dots & f_{0,N-1} & f_{0N}/2 \\ f_{10}/2 & f_{11} & \dots & f_{1,N-1} & f_{1N}/2 \\ \dots & \dots & \dots & \dots & \dots\\ f_{M0}/2 & f_{M1} & \dots & f_{M,N-1} & f_{MN}/2 \end{bmatrix}$$ and the target vector $y=[y_0,\dots,y_M]$.

Let's test it for a simple example. Suppose, $g(x)$ is a Gaussian.

import numpy as np 

def Gaussian(x, mu, sigma):
    return np.exp(-0.5*((x - mu)/sigma)**2)

Discretize the domain $x \in [a,b]$

x = np.arange(-1.0, 1.01, 0.01)
dx = x[1] - x[0]
g = Gaussian(x, 0.25, 0.25)

Let's take sines and cosines with different frequencies as our training functions. Calculating the target vector:

from math import cos, sin, exp
from scipy.integrate import quad

freq = np.arange(0.25, 15.25, 0.25)

y = []
for k in freq:
    y.append(quad(lambda x: cos(k*x)*exp(-0.5*((x-0.25)/0.25)**2), -1, 1)[0])
    y.append(quad(lambda x: sin(k*x)*exp(-0.5*((x-0.25)/0.25)**2), -1, 1)[0])
y = np.array(y)/dx

Now, the regressor matrix:

X = np.zeros((y.shape[0], x.shape[0]), dtype=float)
print('X',X.shape)
for i in range(len(freq)):
    X[2*i,:] = np.cos(freq[i]*x)
    X[2*i+1,:] = np.sin(freq[i]*x)

X[:,0] = X[:,0]/2
X[:,-1] = X[:,-1]/2

Linear regression:

from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, y)
ghat = reg.coef_

import matplotlib.pyplot as plt 

plt.scatter(x, g, s=1, marker="s", label='original g(x)')
plt.scatter(x, ghat, s=1, marker="s", label='learned $\hat{g}$(x)')
plt.legend()
plt.grid()
plt.show()

The Gaussian function is successfully learned although the data are spread somewhat around the true function. The spread is larger where $g(x)$ is close to zero. This spread can be smoothed with a Savitzky-Golay filter

from scipy.signal import savgol_filter
ghat_sg = savgol_filter(ghat, 31, 3) # window size, polynomial order

plt.scatter(x, g, s=1, marker="s", label='original g(x)')
plt.scatter(x, ghat, s=1, marker="s", label='learned $\hat{g}$(x)')
plt.plot(x, ghat_sg, color="red", label='Savitzky-Golay $\hat{g}$(x)')
plt.legend()
plt.grid()
plt.show()

In general, $F[f(x)]$ does not depend linearly on $f(x)$, that is $$F[f(x)]=\int\limits_a^b\mathcal{L}\left(f(x)\right)dx$$ It is still can be written as a function of $f_0, f_1\dots,f_N$ after discretizing $x$ which is also true for the functionals of the form $$F[f(x)]=\int\limits_a^b\mathcal{L}\left(f(x),f'(x)\right)dx$$ because $f'$ can be approximated by a finite differences of $f_0, f_1\dots,f_N$. As $\mathcal{L}$ is a non-linear function of $f_0, f_1\dots,f_N$, one may attempt to learn it with a non-linear method, e.g. neural networks or SVM, although it will probably not be so easy as in the linear case.