9

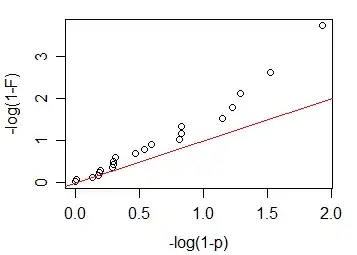
I have multiple individuals, for whom I collected two time series of some parameter. For each individual, I calculated, whether these time series are correlated. So, if I have 20 individuals, as a result I have 20 rho and 20 p-values. Then, I would like to group these values into one group p-value. First, I tried Fisher's method (Wikipedia, MRC wiki).

Here is the MATLAB code example I used, for the sake of reproducibility I provide my input values as well:

pvals = [0.265337997085488
0.00408191031608826
3.39739013503740e-05
0.254982443552454
0.165041294656449
0.416553830442594
0.854810976365062
0.555604221080550
0.256959004076953
0.371337447007835
0.705098835272764
0.122815481253417
0.562862850057724
0.781570743043581
0.248570986138274
0.448488806357779
0.179768419684463
0.560862182877956
0.169198118710575
0.681402534954493
0.723443480957150];
%// pvals is vector of (21,1) shape which holds individual p-values
chi_vals = -2.*log(pvals);
group_pval = 1 - chi2cdf(sum(chi_vals),2*length(pvals));
nsig = sum(pvals < 0.05)

I would have felt that this was enough, but there is something that really got me worried - I get a group p-value of 0.0054, while in my individual p-values there are only 2 values that are "significant" at $p < 0.05$. That doesn't make sense, right? Why is my group p-value so low? Did I make a mistake in calculations or assumptions?

amoeba
  • 93,463
  • 28
  • 275
  • 317
Dmitry Smirnov
  • 635
  • 1
  • 6
  • 11
  • Why would you need to combine them? Looking at the data, it appears there was just two significant correlations. After you correct for multiple comparisons, there might not be any left (did not calculate), or perhaps just the third one. Write that instead to the report. – mmh Jun 23 '15 at 08:10
  • Thank you, even though this doesn't answer my question directly, I like your advice! – Dmitry Smirnov Jun 23 '15 at 09:16
  • 3
    @mmh Your comment would make sense if these were multiple comparisons in one study: then one wishes to correct for multiple testing. HOWEVER the OP is asking how to aggregate repetitions of the same experiment. i.e., a form of meta-analysis. The test Fisher invented for this purpose is sensitive to how far a set of p-values deviates below the expected mean of .5 for a set of p-values drawn from the null (i.e., distributed rectangularly between 0 and 1 by chance). The set provided not only contains one highly significant value, but 1/3rd are p<.2 .8.="" is="" only="" over="" while=""> – tim Apr 06 '16 at 05:05

1 Answers1

7

Your p-value looks to be correct.

Consider that if the null hypothesis is true, p-values should be uniform; when you have many of them, you're effectively checking your collection of p-values for consistency with uniformity, against the alternative that they're smaller than you'd expect from a uniform (Fisher's method measures this degree of being too small in a particular way).

Your values are skewed toward the low side (e.g. consider that 7 values are below 0.25, but only 2 are above 0.75). Fisher's approach can pick up that your p-values tend to be too small.

If the p-values were from a uniform, they should lie close to the red line in this plot (the F values are uniform scores; essentially the ecdf shifted down by $\frac{1}{2n}$ (equivalently the average of the ecdf before and after the point)):

![enter image description here

We can see that the large p-values tend to be too small (they lie left of the line near the top of the plot). Because of that, the Fisher p-value is quite small.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • So, if I understand correctly, the group_pval in my code shows the probability that my pvals come from Uniform(0,1) distribution? Can you suggest alternative way to summarize the individual p-values? Comment above suggested not summarizing, and I see sense in that, but is there still some good way to present just one value for decision? – Dmitry Smirnov Jun 23 '15 at 09:21
  • 3
    No, your group_pval is itself a p-value, and a p-value is *not* the probability the null is true. You can summarize p-values in all manner of ways, depending on how you'd like to summarize them, but the Fisher approach is both the most obvious and the most commonly accepted. You can easily present just one value for a decision; that's what your group_pval *is*. I don't see the difficulty with using it. – Glen_b Jun 23 '15 at 10:10
  • +1 (some time ago). Perhaps it would help to spell out what is `F` in the `-log(F)` on the y-axis of your plot. – amoeba Aug 21 '15 at 21:19
  • @amoeba thanks; updated the plot (there was something wrong with one of my p-values) and added that F is the ecdf (though you can get a very similar plot via uniform scores... using `ppoints` in R). Edit: actually, I have now changed to using ppoints as it avoids an issue with a missing point with using the ECDF – Glen_b Aug 22 '15 at 06:37