I am uncertain how to formally establish that I observe a negative relationship between X and Y in multiple sets of linked data points.
I have analyzed several cells in which values of interest (Y) can be estimated at a variety of distances (X) from its center. In any given cell, I expect Y to decrease at greater distances from the center. Despite the expected negative relationship between X and Y, it could be that Y(x=100) > Y(x=30) if these values are derived from different cells.
Since the individual downward trends (one for each cell) appear to be shifted with respect to one another, I hardly see a negative relationship if I lump all my Y values together. It is important that I consider the linkage between different Y values which originate from the same cell, shown in a single color in the graph below:
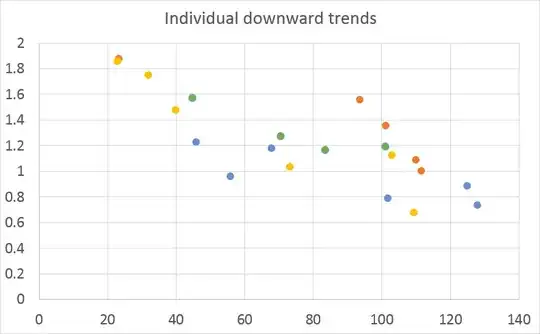
I considered doing a repeated measures ANOVA, but fear this is impossible because the X values for which Y is obtained vary between different cells.
What kind of data transformation or test could I use to establish that, for any given cell, Y tends to decrease as X increases?