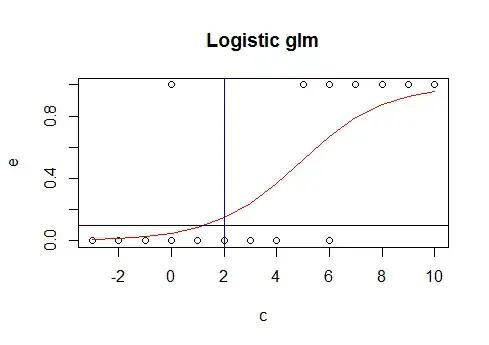
Are there any documented algorithms to separate sections of a given dataset into different curves of best fit?
For example, most humans looking at this chart of data would readily divide it into 3 parts: a sinusoidal segment, a linear segment, and the inverse exponential segment. In fact, I made this particular one with a sine wave, a line and a simple exponential formula.
Are there existing algorithms for finding parts like that, which can then be separately fitted to various curves/lines to make a kind of compound series of best-fits of subsets of the data?
Note that although the example has the ends of the segments pretty much line up, this won't necessarily be the case; there may also be a sudden jolt in the values at a segment cutoff. Perhaps those cases will be easier to detect.
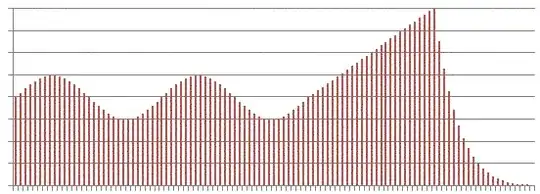
Update: Here is an image of a small bit of real-world data:

Update 2: here is an unusually small real-world set of data (only 509 data points):
4,53,53,53,53,58,56,52,49,52,56,51,44,39,39,39,37,33,27,21,18,12,19,30,45,66,92,118,135,148,153,160,168,174,181,187,191,190,191,192,194,194,194,193,193,201,200,199,199,199,197,193,190,187,176,162,157,154,144,126,110,87,74,57,46,44,51,60,65,66,90,106,99,87,84,85,83,91,95,99,101,102,102,103,105,110,107,108,135,171,171,141,120,78,42,44,52,54,103,128,82,103,46,27,73,123,125,77,24,30,27,36,42,49,32,55,20,16,21,31,78,140,116,99,58,139,70,22,44,7,48,32,18,16,25,16,17,35,29,11,13,8,8,18,14,0,10,18,2,1,4,0,61,87,91,2,0,2,9,40,21,2,14,5,9,49,116,100,114,115,62,41,119,191,190,164,156,109,37,15,0,5,1,0,0,2,4,2,0,48,129,168,112,98,95,119,125,191,241,209,229,230,231,246,249,240,99,32,0,0,2,13,28,39,15,15,19,31,47,61,92,91,99,108,114,118,121,125,129,129,125,125,131,135,138,142,147,141,149,153,152,153,159,161,158,158,162,167,171,173,174,176,178,184,190,190,185,190,200,199,189,196,197,197,196,199,200,195,187,191,192,190,186,184,184,179,173,171,170,164,156,155,156,151,141,141,139,143,143,140,146,145,130,126,127,127,125,122,122,127,131,134,140,150,160,166,175,192,208,243,251,255,255,255,249,221,190,181,181,181,181,179,173,165,159,153,162,169,165,154,144,142,145,136,134,131,130,128,124,119,115,103,78,54,40,25,8,2,7,12,25,13,22,15,33,34,57,71,48,16,1,2,0,2,21,112,174,191,190,152,153,161,159,153,71,16,28,3,4,0,14,26,30,26,15,12,19,21,18,53,89,125,139,140,142,141,135,136,140,159,170,173,176,184,180,170,167,168,170,167,161,163,170,164,161,160,163,163,160,160,163,169,166,161,156,155,156,158,160,150,149,149,151,154,156,156,156,151,149,150,153,154,151,146,144,149,150,151,152,151,150,148,147,144,141,137,133,130,128,128,128,136,143,159,180,196,205,212,218,222,225,227,227,225,223,222,222,221,220,220,220,220,221,222,223,221,223,225,226,227,228,232,235,234,236,238,240,241,240,239,237,238,240,240,237,236,239,238,235
Here it is, charted, with the appoximate position of some known real-world element edges marked with dotted lines, a luxury we won't normally have:

One luxury we do have, however, is hindsight: the data in my case is not a time series, but is rather spatially related; it only makes sense to analyse a whole dataset (usually 5000 - 15000 data points) at once, not in an ongoing manner.