I want to run a Mann-Whitney test on 2 arbitrary sets of data but I read that one of the assumptions of the Mann-Whitney test is that the data is the same shape. How can I test if the 2 sets of data are the same shape?
I'm automating a test on Python so a link to a relevant python package would help. I would also like to know if there is no straightforward way of doing this thanks.
The test does not require the assumption that the data has the same shape. Without any assumptions, Mann-Whitney tests if the distribution of $X$ and $Y$ are the same:
$$H_0: F_x = F_y, H_1:F_x \neq F_y. $$
In order to test equality of medians the following assumption is required. There is only a shift location between the two distributions, $F_X(x) = F_Y(x + \delta)$ under $H_1$. To check for this assumption you can look at the difference between the quantiles they should all be around $\delta$, it can be done visually using qq-plot. If the assumption does not hold, the test is no longer valid (p-value under the null will be stochastically smaller than uniform).
Example: We compare two samples sampled from Normal distribution $X \sim N(0, 1)$ and $Y \sim N(0, 10^2)$, at each iteration we apply the Mann-Whitney test and save the p-value. Finally, we inspect the p-value distribution.
pvals <- rep(NA, 1000)
for (i in 1:1000) {
x <- rnorm(30, 0, 1)
y <- rnorm(30, 0, 10)
pvals[i] <- wilcox.test(x, y)$p.value
}
qqplot(pvals, qunif(ppoints(500)), type = 'l')
abline(a = 0, b = 1, col = 'red', lwd = 2)
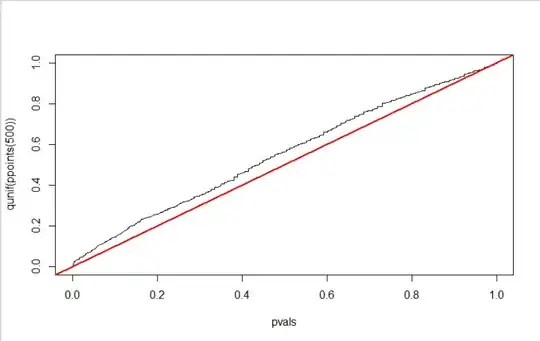
As can be seen the two distribution are different, but have the same median. IF the we test equality of medians the test is not valid, however if we are testing equality of distributions it is. However, it has very low power in this specific scenario. It is better used to detect differences between distribution where one is stochastically larger / smaller than the other.
