0

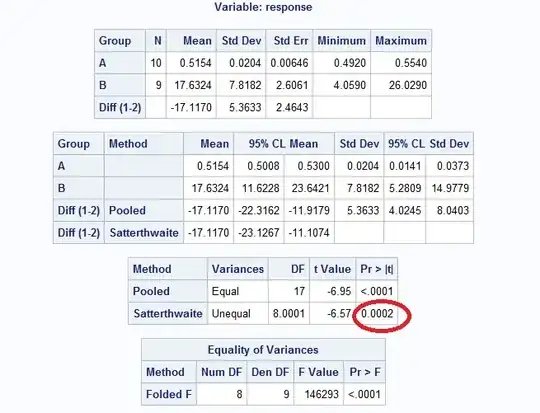
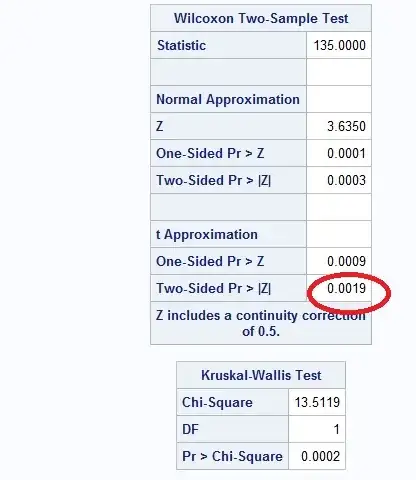
I am trying to find if there is any difference in performance between two sampled groups. 

Sample A
# Users response time(sec)
1900    0.541
3800    0.507
5700    0.492
7600    0.494
9500    0.514
7600    0.494
13300   0.515
16000   0.52
18000   0.554
20000   0.523

Sample B
# Users Response time(sec)
1500    4.059
3000    8.336
4500    12.362
6000    17.003
7500    19.695
8987    23.771
10487   22.369
11912   26.029
13499   25.068

Sample A has a list of response time like sample B. Now I want to statistically test whether or not there is a difference in response time between sample A and sample B. I checked that these samples are not normally distributed.

H0: No significant difference in response time between Sample A and sample B

TMNT
  • 41
  • 4
  • 5
    Does the first line mean there were 1900 individual samples and the average response time is 0.541s? or the 1900th sample had a response time of 0.541s? – Eric Farng May 27 '15 at 22:29

2 Answers2

1

Wilcoxon rank-sum test if the samples are not normally distributed.

Transformation seems not suitable in this case because of the small sample sizes.

Yim Yik-Man
  • 11
  • 2
0

I think both t-test and wilcoxon test will be ok for your data.

Data a;
input Group $ response;
datalines;
A    0.541
A   0.507
A    0.492
A    0.494
A   0.514
A    0.494
A   0.515
A   0.52
A   0.554
A   0.523

B    4.059
B    8.336
B    12.362
B    17.003
B    19.695
B    23.771
B   22.369
B   26.029
B   25.068
;
run;
proc ttest data=a;
class group;
var response;
run;

proc npar1way data=a wilcoxon;
class group;
var response;
run;

Results: enter image description here

enter image description here

Community
  • 1
Deep North
  • 4,527
  • 2
  • 18
  • 38
  • Why t-test? The poster said the data can't be assumed for normal? – SmallChess May 28 '15 at 12:00
  • The student theorem says $\bar{X}$ have a $N(\mu, \sigma^2)$. (Robert hogg Introduction mathematical statistics). I think the sample size for n=10 and n=9 might be Ok enough for using CLT to assume that $\bar{X}s$ are normal distributed. – Deep North May 28 '15 at 13:48
  • Sorry, $\bar{X} $ have a $N(\mu, \sigma^2/n)$ – Deep North May 28 '15 at 14:02
  • CLT only gives guarantees a normal for a sufficient large sample size. The question here is a small sample size. At such sample size, the distribution is less likely to be normal and violate the t-test assumption. The sample size is about 10, which is too small for a good normal approximation, in particular if the data is non-normal itself. See https://en.wikipedia.org/wiki/Student's_t-test#Assumptions – SmallChess May 28 '15 at 14:10
  • I think a non-parametric test is a better alternative. It'll give better power. – SmallChess May 28 '15 at 14:11
  • I think the discussion here might be helpful http://stats.stackexchange.com/questions/9573/t-test-for-non-normal-when-n50?s=2|1.0692 – Deep North May 29 '15 at 00:46
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/24236/discussion-between-deep-north-and-student-t). – Deep North May 29 '15 at 00:47