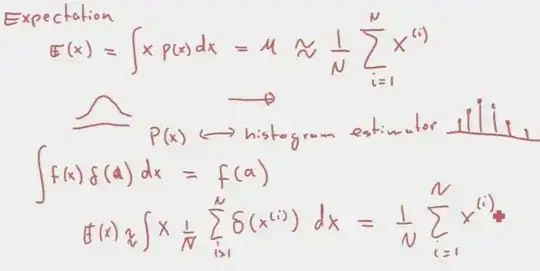
I'm having some trouble understanding this slide. It's mentioned in the context of gaussian distributions.
I sort of understand the Dirac delta "function". The main difficulty I'm having is with the summation over the delta functions.
1) How does it replace the probability distribution p(x)? Is it not just a scalar?
2) How do we go from the left equation to the one on the right?