I'm curious to know how important the bias node is for the effectiveness of modern neural networks. I can easily understand that it can be important in a shallow network with only a few input variables. However, modern neural nets such as in deep learning often have a large number of input variables to decide whether a certain neuron is triggered. Would simply removing them from, e.g., LeNet5 or ImageNet have any real impact at all?
- 132,789
- 81
- 357
- 650
- 4,626
- 10
- 38
- 73
-
@gung - I've seen you've edited the title to use the phrase "bias node". I am curious as to why you prefer that title? I've never heard that usage before. Moreover, it seems confusing to use the word "node" when the bias is not a separate node in a network. – pir Dec 27 '15 at 00:43
-
2If you dislike it, you can roll back the edit w/ my apologies. I always thought the name was fairly standard, although I haven't played w/ ANNs in years & some call it the "bias neuron" instead. FWIW, "bias" is a bit ambiguous in statistics / ML; it most commonly refers to an estimator whose sampling distribution is not centered on the true value of the parameter, or a predictive function / predicted value that differs from the true function / mean, etc., whereas the bias node is a specific part of an ANN. – gung - Reinstate Monica Dec 27 '15 at 00:52
-
2It is an actual node--at least in the sense that any of them are--in the network. Eg, see the black nodes in [this image](http://tech-algorithm.com/uploads/image001.png). – gung - Reinstate Monica Dec 27 '15 at 00:53
-
Okay, that makes sense - it is true that "bias" is quite ambiguous. Thanks for the explanation. – pir Dec 28 '15 at 15:54
-
1For neurons the bias unit seems expontaneous firing, this happens in nature. – user3927612 Jan 28 '16 at 23:54
3 Answers
Removing the bias will definitely affect the performance and here is why...
Each neuron is like a simple logistic regression and you have $y=\sigma(W x + b)$. The input values are multiplied with the weights and the bias affects the initial level of squashing in the sigmoid function (tanh etc.), which results the desired the non-linearity.
For example, assume that you want a neuron to fire $y\approx1$ when all the input pixels are black $x\approx0$. If there is no bias no matter what weights $W$ you have, given the equation $y=\sigma(W x)$ the neuron will always fire $y\approx0.5$.
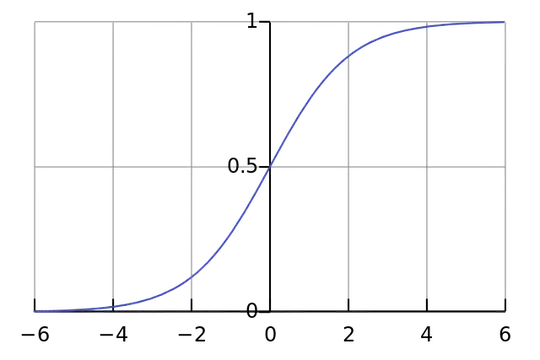
Therefore, by removing the bias terms you would substantially decrease your neural network's performance.
- 3,057
- 17
- 25
-
2Thanks, that makes some sense. I guess that even though most modern nets use ReLU as the activation function (see e.g. http://papers.nips.cc/paper/4824-imagenet), this could still be relevant if the net needed to fire when all the input pixels are black. ReLU is defined as f(x) = max(0, x). – pir May 25 '15 at 20:41
-
-
Can anybody please explain how come y will always output .5 irrespective of weights? Are you saying neuron will output .5 or neuton will fire at .5 instead of 1. Im confused – shalini Jun 03 '15 at 10:44
-
4The plot depicts the activations of a sigmoid neuron given the input. Now assume that we want a neuron to fire $y\approx1$ when all pixels are black $x\approx0$. This would be impossible without the bias term and when $x\approx0$ it will always fire $y\approx0.5$. – Yannis Assael Jun 03 '15 at 14:39
-
2While I agree with the theory, it is worth pointing out that with modern large nets the chances of getting an all-zero input is negligible. This also relies on the assumption that a net would want to fire a 1 - deep nets will most likely not care about the single neuron output - this is partly why *dropout* is so popular for regularizing nets. – Max Gordon Dec 26 '15 at 23:34
-
2@MaxGordon is right. This answer doesn't apply to this question. Try removing the bias from a big network and you'll see that it makes very little difference. – Neil G Jan 29 '16 at 01:46
-
see this answer for a nice visualization of why the bias is important http://stackoverflow.com/questions/2480650/role-of-bias-in-neural-networks – fabrizioM Apr 15 '16 at 07:50
-
@fabrizioM that network has 3 nodes. The question says "modern neural nets such as in deep learning often have a large number of input variables to decide whether a certain neuron is triggered. Would simply removing them from, e.g., LeNet5 or ImageNet have any real impact at all?" – Neil G Apr 26 '16 at 17:07
I disagree with the other answer in the particular context of your question. Yes, a bias node matters in a small network. However, in a large model, removing the bias inputs makes very little difference because each node can make a bias node out of the average activation of all of its inputs, which by the law of large numbers will be roughly normal. At the first layer, the ability for this to happens depends on your input distribution. For MNIST for example, the input's average activation is roughly constant.
On a small network, of course you need a bias input, but on a large network, removing it makes almost no difference. (But, why would you remove it?)
- 13,633
- 3
- 41
- 84
I'd comment on @NeilG's answer if I had enough reputation, but alas...
I disagree with you, Neil, on this. You say:
... the average activation of all of its inputs, which by the law of large numbers will be roughly normal.
I'd argue against that, and say that the law of large number necessitates that all observations are independent of each other. This is very much not the case in something like neural nets. Even if each activation is normally distributed, if you observe one input value as being exceptionally high, it changes the probability of all the other inputs. Thus, the "observations", in this case, inputs, are not independent, and the law of large numbers does not apply.
Unless I'm not understanding your answer.
- 141
- 4