The question has been asked a while ago but I think people are still tumbling across it. For me it helped to know about the mathematical background to understand batching and where the advantages/disadvantages mentioned in itdxer's answer come from. So please take this as a complementary explanation to the accepted answer.
Consider Gradient Descent as an optimization algorithm to minimize your Loss function $J(\theta)$. The updating step in Gradient Descent is given by
$$\theta_{k+1} = \theta_{k} - \alpha \nabla J(\theta)$$
For simplicity let's assume you only have 1 parameter ($n=1$), but you have a total of 1050 training samples ($m = 1050$) as suggested by itdxer.
Full-Batch Gradient Descent
In Batch Gradient Descent one computes the gradient for a batch of training samples first (represented by the sum in below equation, here the batch comprises all samples $m$ = full-batch) and then updates the parameter:
$$\theta_{k+1} = \theta_{k} - \alpha \sum^m_{j=1} \nabla J_j(\theta)$$
This is what is described in the wikipedia excerpt from the OP. For large number of training samples, the updating step becomes very expensive since the gradient has to be evaluated for each summand.
Stochastic Gradient Descent
In Stochastic Gradient Descent one computes the gradient for one training sample and updates the paramter immediately. These two steps are repeated for all training samples.
for each sample j compute:
$$\theta_{k+1} = \theta_{k} - \alpha \nabla J_j(\theta)$$
One updating step is less expensive since the gradient is only evaluated for a single training sample j.
Difference between both approaches
Updating Speed: Batch gradient descent tends to converge more slowly because the gradient has to be computed for all training samples before updating. Within the same number of computation steps, Stochastic Gradient Descent already updated the parameter multiple times. But why should we then even choose Batch Gradient Descent?
Convergence Direction: Faster updating speed comes at the cost of lower "accuracy". Since in Stochastic Gradient Descent we only incorporate a single training sample to estimate the gradient it does not converge as directly as batch gradient descent. One could say, that the amount of information in each updating step is lower in SGD compared to BGD.
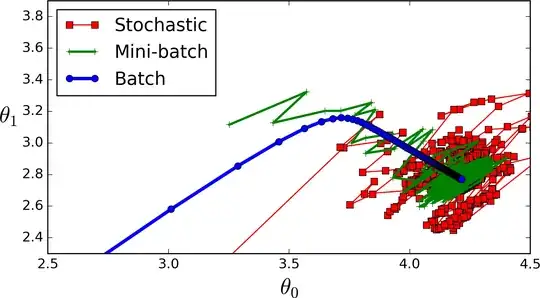
The less direct convergence is nicely depicted in itdxer's answer. Full-Batch has the most direct route of convergence, where as mini-batch or stochastic fluctuate a lot more. Also with SDG it can happen theoretically happen, that the solution never fully converges.
Memory Capacity: As pointed out by itdxer feeding training samples as batches requires memory capacity to load the batches. The greater the batch, the more memory capacity is required.
Summary
In my example I used Gradient Descent and no particular loss function, but the concept stays the same since optimization on computers basically always comprises iterative approaches.
So, by batching you have influence over training speed (smaller batch size) vs. gradient estimation accuracy (larger batch size). By choosing the batch size you define how many training samples are combined to estimate the gradient before updating the parameter(s).