Understanding "the kernel has zero mean"

Question

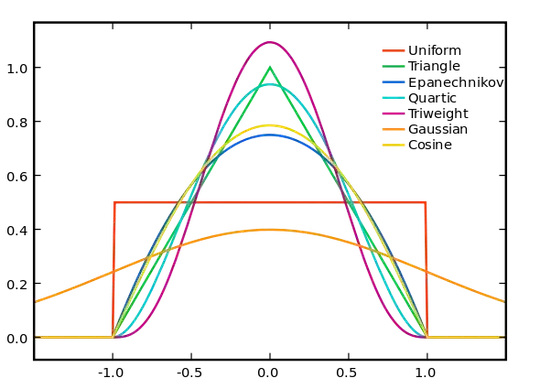
I am trying to understand kernel density estimation and found the graphic below illustrating different kernel functions on Wikipedia. I have no trouble reconciling it with the two statements

"the kernel integrates to one", i.e. $\int K(z)\mathrm{d}z=1$, and
"the kernel is symmetric around zero", i.e. $K(z)=K(-z)$.

But I've several times seen the statement "the kernel has zero mean" and I can't make sense out of it.

Does it mean

$\mathbb{E}[K(z)]=\int K(z)z\mathrm{d}z=0$ or
something else entirely?

Some common kernels

Why this property of zero mean of a kernel is important in kernel density estimation? — Vladislavs Dovgalecs, May 17 '15 at 05:11
@xeon Otherwise, the convolution of the kernel with a distribution changes the location. That can be compensated by subtracting the kernel's mean from the result--which is identical to centering the kernel at a zero mean in the first place. So, no importance whatsoever is attached to having a zero mean, but it is useless to have a nonzero mean. — whuber, May 19 '15 at 20:36
Note that symmetry (property 2) together with the existence of a first moment of $K$ implies that moment must be zero: http://stats.stackexchange.com/questions/46843. — whuber, May 19 '15 at 20:39

score 6 · Accepted Answer · edited Apr 13 '17 at 12:44

The first statement is almost, but not entirely correct. $K$ is a density function and what we mean when we refer to the mean of the density function $K$ is $$\int K(z)z\mathrm{d}z.$$ Similarly, the variance of $K$ is $$\int K(z)z^2\mathrm{d}z.$$ So, it doesn't make any sense to write $\mathbb{E}[K(z)]$. Rather, the statement "the kernel has zero mean" should be formally written as $$\int K(z)z\mathrm{d}z=0.$$ (Thanks, Glen_b!)

Understanding "the kernel has zero mean"

1 Answers1