6

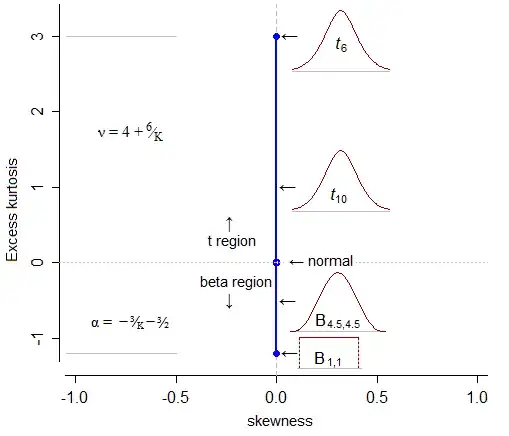
I am aiming to run simulations in order to estimate the influence of the distribution of $Y$ (independent variable) on a certain binary outcome $X$ (dependent variable). $Y$ must always has a mean of 0 and must be symmetric (skew = 0) but I'd like to vary independently the variance (eventually from 1 to 250) and the kurtosis (from a square to a narrow peak, eventually from -1.2 to 3) of $Y$.

I've been looking at a variety of distributions but I found none that seemed suited for this kind purpose.

Can you help me choosing a distribution from which I can easily change the variance and kurtosis while keeping the mean and the skew at zero?

EDITS

More descriptions

I realized there were still open questions (not that many though). My preferences are:

  • mean = 0
  • variance: can vary
  • symmetric: Yes (I didn't realized at first that skew=0 doesn't imply symmetry)
  • kurtosis: can vary independently of the variance
  • number of modes: unimodal (not strict on this issue)
  • Bounded: Doesn't matter.
  • continuous/discrete: Doesn't matter. I will have to take a discrete approximations if it is continuous but I don't mind
  • Tail Behaviour: I am quite interested in the impact of the tail. I thought that by allowing kurtosis to change was enough as a description but maybe I should describe higher moments...

Context

I am working in the field of population genetics and I am interested in the influence of the variance and kurtosis of the dispersal kernel ($Y$) on the probability of fixation of a given allele ($X$). I am not interested to simulate cases where the distribution of dispersal is skewed and the mean should always be at the position of the deme of the parents (this can very easily solved by a simple addition anyway). Previous studies have argued (without showing any evidence) that variance and kurtosis are important and empirical studies showed that the dispersal kernel is often leptokurtic. Not sure I correctly addressed your comment. Did I? Thank you

Remi.b
  • 4,572
  • 12
  • 34
  • 64
  • It is a little surprising that skewness and kurtosis would provide adequate controls over any kind of influence in a regression situation. What is the reason you are performing your analysis in this particularly constrained way, especially since you otherwise haven't any preferences for the distributional shape? – whuber May 15 '15 at 16:20
  • You could have used the $t_\nu$-distribution, but that will not give you negative kurtosis ... – kjetil b halvorsen May 15 '15 at 16:23
  • @whuber I am working in the field of population genetics and I am interested in the influence of the variance and kurtosis of the dispersal kernel ($Y$) on the probability of fixation of a given allele. I am not interested to simulate cases where the distribution of dispersal is skewed and the mean should always be at the position of the deme of the parents (this can very easily solved by a simple addition anyway). – Remi.b May 15 '15 at 16:32
  • @whuber Previous studies have argued (without showing any evidence) that variance and kurtosis are important and empirical studies showed that the dispersal kernel is often leptokurtic. Not sure I correctly addressed your comment. Did I? Thank you – Remi.b May 15 '15 at 16:32
  • It's good to know that there is some basis for this approach so that you're not going off in an unfruitful direction. That still leaves you with a rather diffuse question, because there are myriad ways to solve it. That, perhaps, is a luxury, because it means you may impose additional constraints on the solution. For instance, must the distribution be unimodal? Perfectly symmetric or only with zero skewness (the former is much more restrictive)? Bounded in either direction or not? If unbounded, what should be the tail behavior? Continuous or not? Etc, etc. – whuber May 15 '15 at 16:39
  • note re your title: specifying "skew=0" doesn't guarantee symmetry. If you want symmetry, you should probably say it that way rather than "skew=0". – Glen_b May 15 '15 at 16:42
  • Thanks a lot for your comments. It already help a lot! Please see edits in the post. – Remi.b May 15 '15 at 16:51
  • According to the last bullet, you are interested in the effects of the tail. The kurtosis criterion is weak in that regard: it merely causes the tail eventually to be $o(x^{-5})$, but that covers a lot of ground. You might want to specify the possible tail behaviors more explicitly. For instance, you might wish to explore the effects of rapid decrease ($\exp(-x^2)$ behavior), exponential decrease ($\exp(-x)$ behavior), and polynomial decrease ($x^{-\gamma}$ behavior). It is rare for one parametric family to include all such behaviors, so a more flexible approach might be warranted. – whuber May 15 '15 at 17:46
  • 1
    I would love to have distributions which tail is very long (uniform-looking tail) at one extreme and distributions which tail is pretty much inexistent (the function reaches the axis density/mass = 0 with a slope of -infinite). I don't quite have the tools to make more of an accurate description of the tail. Previous similar work compared a normal distribution to a [Laplace distribution](http://en.wikipedia.org/wiki/Laplace_distribution) (exponential decrease). – Remi.b May 15 '15 at 18:01

2 Answers2

5

There are many possibilities. One possibility is to take a pair of families to cover positive and negative excess kurtosis, and when matching the first four moments the obvious candidates are Pearson-family distributions.

The family of scaled t-distributions have parameters ($\sigma$ and $\nu$) that affect the variance and kurtosis. They can only have kurtosis above that of the normal, though.

That will have excess kurtosis $\frac{6}{\nu-4}$ (so if you want that to only go as high as 3, you'll want $\nu\geq 6$).

It has variance $\sigma^2 \frac{\nu}{\nu-2}$, so given $\nu$ you can choose $\sigma$ to yield the desired variance

The family of scaled shifted (to mean 0) beta distributions then would take care of the case where kurtosis was smaller than for the normal (both families include the normal as a limiting case). So take a $\text{Beta}(\alpha,\alpha)$ and shift it down by $\frac{1}{2}$ and then scale to the desired variance.

That is a $\text{Beta}(\alpha,\alpha)$ has excess kurtosis $-\frac{6}{ (2\alpha + 3)}$, and includes your desired uniform at $\alpha=1$.

Before scaling it has variance $\frac{1}{4(2\alpha+1)}$; the ratio of the desired variance to that unscaled variance will be the square of the required scale.

enter image description here

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Using the beta distribution, if I want mean=0, skew=0, variance=V, kurtosis=K, then I need the distribution $\text{Beta}(\alpha, \alpha) 2 \sqrt{V + 2 \alpha V} - \frac{1}{2}$, where $\alpha = - \frac{3}{K-2}$ and this is going to work for any $V \text{ element of } (-\infty, +\infty)$ and for any $K \text{ element of } [-1.2, 3]$. Did I get it right? – Remi.b May 15 '15 at 17:34
  • I believe you've made a calculation error. If $K = -\frac{6}{ (2\alpha + 3)}$ then $\alpha$ is not $-\frac{3}{ (K-2)}$ (I didn't check past that, since that will affect later calculation). The general sort of idea is right though. However, the symmetric beta will only give you negative excess kurtosis, $K<0$. That's why there's the $t$ for $K>0$ – Glen_b May 16 '15 at 01:17
  • I've included the $\nu$ and $\alpha$ parameters in terms of excess kurtosis, $K$ in a diagram showing the basic idea. – Glen_b May 16 '15 at 02:22
  • Ok, that makes sense to me now! Thanks a lot @Glen_b – Remi.b May 16 '15 at 17:55
3

Have a look at heavy tail Lambert W x F distributions (disclaimer: I am the author). The random variable $Y \sim Lambert W \times F$ is a heavy-tail version of $X\sim F$, where you control the tails with tail parameter $\delta \geq 0$: for $\delta = 0$, $X = Y$ and thus Lambert W x F is the same as F; and for $\delta \rightarrow \infty$ you get more and more heavy tails in $Y$ (Tukey's h is a special case of Lambert W x F random variables for F = Gaussian and $\alpha = 1$).

Note that this works for any (non pathological) continuous distribution -- not just the Normal distribution.

For your particular request of mean = 0, symmetric, and variable variance and kurtosis you can set $\mu = 0$, $\delta_{\ell} = \delta_r = \delta$ (by default), and vary scale $\sigma$ and tail parameter $\delta$.

In R this is implemented in the LambertW package (use type = "h" and distname = "normal").

See also (my) related replies here:

Community
  • 1
Georg M. Goerg
  • 2,364
  • 20
  • 21