My question:
Imagine $d$ identical lotteries. Each individual lottery picks a cost $c_{i}$ between $0$ and $1$. Picking a costs occurs with probability distribution $f(c)$. The total cost of these $d$ units is $a=\sum_{i=1}^{d} c_{i}$.
What is the probability distribution for $a$, i.e. what is $\tilde{f}(a)$? This should be defined from $0$ to $d$.
If it helps, assume $f(c)=\gamma c^{\gamma-1}$ and $F(c)=\int_{0}^{c} f(c')dc'=c^{\gamma}$, as depicted in the following figure.

This problem comes from the article McNerney et al. "Role of design complexity in technology improvement" found on page 4 of the Supporting Information at [http://www.pnas.org/content/108/22/9008.full?tab=ds].
My first attempt:
The first step I took, following the article cited above, was to define $\tilde{f}(a)=\idotsint_{start}^{stop}f(c_{1}) \cdots f(c_{d}) \, \delta(a-c_{1}- \cdots -c_{d}) \, dc_{1} \cdots dc_{d}$.
However, what are the correct values for $start$ and $stop$? As each $c$ and $f(c)$ is defined over $0$ to $1$, these seem reasonable $start$ and $stop$ values. However, this runs into a problem.
Imagine, first of all, the $d=2$ scenario. If $a<1$, for example, $a=0.5$, then doing the first integral leads to $\tilde{f}(0.5)=\int_{0}^{1}f(c_{1})f(0.5-c_{1})dc_{1}$. This leads to integrating over $f(c)$ for negative values of the argument $c$, where $f(c)$ is not defined. A solution would be to reduce $stop$ to $a$.
If $a>1$, for example, $a=1.5$, then doing the first integral leads to $\tilde{f}(1.5)=\int_{0}^{1}f(c_{1})f(1.5-c_{1})dc_{1}$. This leads to integrating over $f(c)$ for too high values of the argument $c$, where $f(c)$ is not defined. A solution would be to increase $start$ to $a-1$.
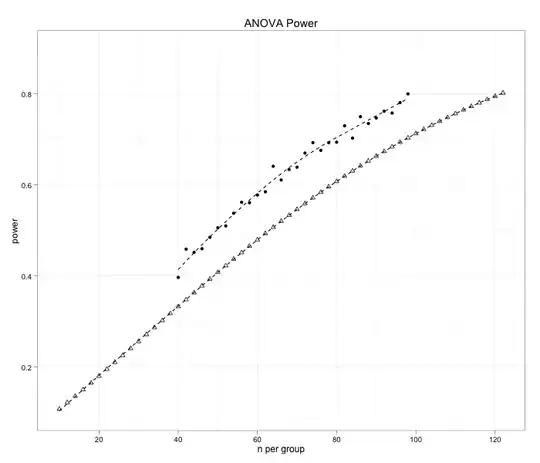
For $d=3$, the problem become even more complex. If $a<1$, a similar problem with integrating over too low values occurs. If $a>2$, a similar problem with integrating over too high values occurs. If $1<a<2$, then both the $start$ and the $stop$ need to be adjusted to prevent the integration from going into undefined areas.
My second attempt:
Find out for each value of $a$ the number of ways in which $d$ different $c$'s, where each $c$ is between $0$ and $1$, can sum up to this value of $a$. Then multiply this probability with $f(c)$ to arrive, in some way, at $\tilde{f}(a)$. However, I am unsure about the details.
Numerical simulations using Mathematica give the following plots:
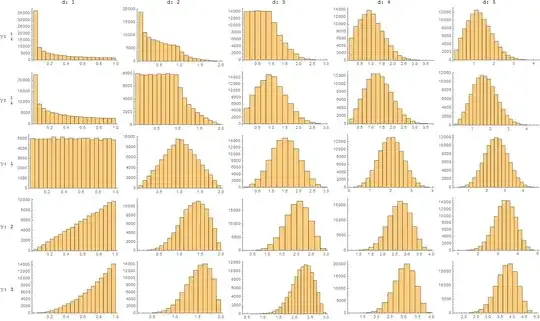
myFInverse[f_,\[Gamma]_]:=f^(1/\[Gamma])
myRandomTable[d_,n_,\[Gamma]_]:=Table[myFInverse[RandomReal[1,d],\[Gamma]],{i,1,n}]
Grid[Prepend[MapThread[Prepend,{Table[Histogram[Total[myRandomTable[d,100000,\[Gamma]],{2}],ImageSize->250],{\[Gamma],{1/3,1/2,1,2,3}},{d,1,5}],Table["\[Gamma]: "<>ToString[\[Gamma],StandardForm],{\[Gamma],{1/3,1/2,1,2,3}}]}],Prepend[Table["d: "<>ToString[d],{d,1,5}],""]]]