Difference between regression analysis and curve fitting

Question

Can anybody please explain to me the real difference(s) between regression analysis and curve fitting (linear and nonlinear), with an example if possible?

It seems that both try to find a relationship between two variables (dependent vs independent) and then determine the parameter (or coefficient) associated with the models being proposed. For example, if I have a set of data like:

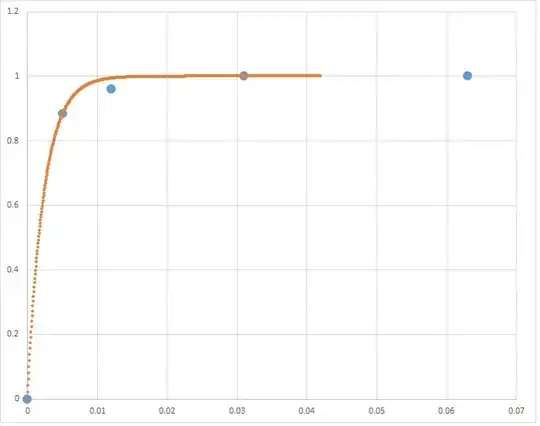
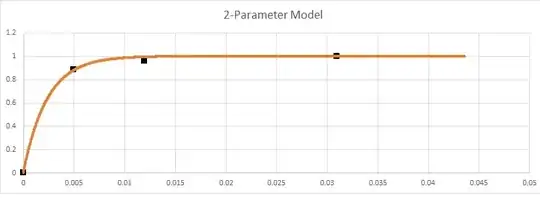
Y = [1.000 1.000 1.000 0.961 0.884 0.000] 
X = [1.000 0.063 0.031 0.012 0.005 0.000]

Can anybody suggest a correlation formula between these two variables? I am having a difficulty understanding the difference between these two approaches. If you prefer to support your answer with other data sets, it's OK since that one seems hard to fit (perhaps only for me).

The above data set represents the $x$ and $y$ axes of a receiver operating characteristic (ROC) curve, where $y$ is the true positive rate (TPR) and $x$ is the false positive rate (FPR).

I am trying to fit a curve, or do a regression analysis as per my original question, not sure yet, among these points to estimate the TPR for any particular FPR (or vice-versa).

First, is it scientifically acceptable to find such a curve fitting function between two independent variables (TPR and FPR)?

Second, is it scientifically acceptable to find such a function if I know that the distributions of the actual negative and the actual positive cases are not normal?

Answer 1

I doubt that there is a clear and consistent distinction across statistically minded sciences and fields between regression and curve-fitting.

Regression without qualification implies linear regression and least-squares estimation. That doesn't rule out other or broader senses: indeed once you allow logit, Poisson, negative binomial regression, etc., etc. it gets harder to see what modelling is not regression in some sense.

Curve-fitting does literally suggest a curve that can be drawn on a plane or at least in a low-dimensional space. Regression is not so bounded and can predict surfaces in a several dimensional space.

Curve-fitting may or may not use linear regression and/or least squares. It might refer to fitting a polynomial (power series) or a set of sine and cosine terms or in some other way actually qualify as linear regression in the key sense of fitting a functional form linear in the parameters. Indeed curve-fitting when nonlinear regression is regression too.

The term curve-fitting could be used in a disparaging, derogatory, deprecatory or dismissive sense ("that's just curve fitting!") or (almost the complete opposite) it might refer to fitting a specific curve carefully chosen with specific physical (biological, economic, whatever) rationale or tailored to match particular kinds of initial or limiting behaviour (e.g. being always positive, bounded in one or both directions, monotone, with an inflexion, with a single turning point, oscillatory, etc.).

One of several fuzzy issues here is that the same functional form can be at best empirical in some circumstances and excellent theory in others. Newton taught that trajectories of projectiles can be parabolic, and so naturally fitted by quadratics, whereas a quadratic fitted to age dependency in the social sciences is often just a fudge that matches some curvature in the data. Exponential decay is a really good approximation for radioactive isotopes and a sometimes not too crazy guess for the way that land values decline with distance from a centre.

Your example gets no explicit guesses from me. Much of the point here is that with a very small set of data and precisely no information on what the variables are or how they are expected to behave it could be irresponsible or foolish to suggest a model form. Perhaps the data should rise sharply from (0, 0) and then approach (1, 1), or perhaps something else. You tell us!

Note. Neither regression nor curve-fitting is limited to single predictors or single parameters (coefficients).

Answer 2

In addition to @NickCox's excellent answer (+1), I wanted to share my subjective impression on this somewhat fuzzy terminology topic. I think that a rather subtle difference between the two terms lies in the following. On one hand, regression often, if not always, implies an analytical solution (reference to regressors implies determining their parameters, hence my argument about analytical solution). On the other hand, curve fitting does not necessarily imply producing an analytical solution and IMHO often might be and is used as an exploratory approach.

Answer 3

As there already seems to be an adequate array of explanations of Regression Analysis vs Curve Fitting, I’ll leave that alone. However, there is an additional question buried in the OP’s original question. There’s very little ‘given data’, but he asked if someone could suggest a correlation formula, so I’ll add my 2 cents.

I don’t have any experience with ROC Curves etc..., however, plotting the data gives a strong indication that it’s a First-Order System $\frac{1}{\tau\centerdot s+1}$ (in Laplace terminology) responding to a Step-Input $\frac{1}{s}$ (in Laplace terminology). Obviously, the time constant is very small, yielding an extremely fast steady-state. I’ll assume that the dependent variable is ‘y’, and the independent variable is ‘t’.

A general equation for a 1st order process is $y=A[1 – B \centerdot e^ {-\frac {t}{\tau}}]$, where $\tau$ is the process time constant (where 1 $\centerdot\tau$ generates approx 63.2% of the response).

Using your data, $@t=\infty, y=1$, therefore, $A=1$. The general model now becomes $y=1 – B \centerdot e^ {-\frac {t}{\tau}}$.

In addition, $@t=0, y=0$, therefore $B=1$. The model is now $y=1 – e^ {-\frac {t}{\tau}}$.

Regressing (or curve fitting) your data to this equation yields $y=1 – e^ {-\frac {t}{0.0023}}$. Explicitly, this says that in $\approx 0.0023\space sec$, 63.2% of the response has completed.

I have the benefit of not knowing your specific noise or data variance, so I took the liberty to curve fit a 2-parameter model to see if it tightens the error. That yielded the model $y=1 – 0.99972 \centerdot e^ {-\frac {t}{0.0023}}$.

I’d recommend taking more data on the early portion of the response, and ignore sampling after the response lines out, as there’s nothing interesting to model at steady-state. In addition, the $exp()$ argument is getting extremely high the further you go out into steady-state.