5

I am using emcee to do inference on some data. I am trying to fit my data to a line of equation $ y = mx + b $.

# Initialize MCMC
ndim = 2 # number of parameters in the model
nwalkers = 100 # number of MCMC walkers
nsteps = 500 # number of MCMC steps

I did a plot to visualize the time series of the parameters in the chain. The figure below shows the positions of each walker as a function of the number of steps in the chain:

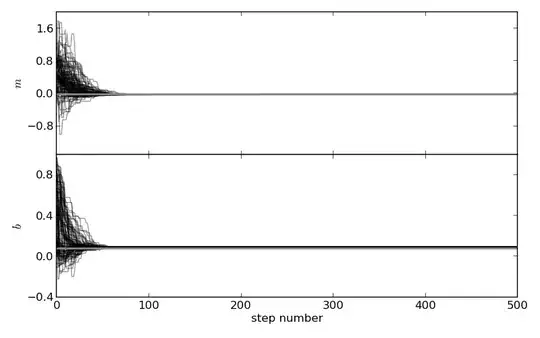
enter image description here

The gray horizontal line represents the values of m and b I got from doing classical linear regression without taking the uncertainties of my parameters into consideration.

My question is can I trust this graph? It converges "very quickly". According to some researches, I should burn-in approx the first half of the steps!

In order to better analyze this graph, I checked the acceptance fraction of each of the 100 walkers, the result is:

0.63   0.632  0.64   0.668  0.642  0.612  0.65   0.67   0.61   0.612
0.64   0.632  0.63   0.636  0.604  0.618  0.62   0.662  0.646  0.612
0.63   0.618  0.642  0.634  0.608  0.658  0.614  0.62   0.658  0.698
0.662  0.64   0.652  0.638  0.596  0.654  0.66   0.646  0.69   0.644
0.628  0.638  0.706  0.644  0.638  0.62   0.608  0.64   0.584  0.654
0.658  0.652  0.658  0.684  0.64   0.668  0.632  0.634  0.628  0.632
0.63   0.612  0.598  0.64   0.58   0.632  0.596  0.618  0.648  0.644
0.622  0.632  0.64   0.656  0.658  0.648  0.632  0.628  0.66   0.592
0.654  0.602  0.652  0.616  0.654  0.646  0.632  0.636  0.656  0.63
0.624  0.662  0.636  0.66   0.614  0.676  0.64   0.656  0.642  0.55

The acceptance rate should be between 0.25 and 50, right? It looks like my acceptance rate is higher than that.

I would like to know your opinion on this problem. Thanks!

Edit

I have 373 data points. And my likelihood is: $$ p(D|\theta) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\frac{(y - mx - b)^2}{\sigma^2}} $$ where $\sigma$ represents the uncertainties in my $y$ data points.

aloha
  • 410
  • 2
  • 9
  • what are the prior distributions that you are sampling from? – Eric May 01 '15 at 18:46
  • @Eric, the code that I wrote is a "toy model" to better understand how the package `emcee` works. So basically I am using uniform priors. – aloha May 01 '15 at 19:04
  • We lack details: size of your data, version of your proposal, for instance. Having an acceptance rate of 60% has nothing terrible about it. And most MCMC chains do not need a burn-in at all. The only unusual feature in your output is the lack of variability of the chains over the remaining iterations. – Xi'an May 01 '15 at 19:48
  • @Xi'an, please check the update. I thought I should always do a burn-in. Thanks for the clarification! – aloha May 01 '15 at 19:56
  • @Xi'an, I change the scale parameter (the default was 2.0). When I decrease this value to 0.001 the iterations converge after ~ 300 steps but the acceptance rates decrease dramatically to 0.015 - 0.03. – aloha May 01 '15 at 20:17
  • When I increase it to 5, the number of iterations needed to converge are same as above, ~ 50 steps and the acceptance ratio is ~ 0.3-0.44. – aloha May 01 '15 at 20:19
  • This is as should be. So you can increase your MCMC scale just enough to reach a 25% acceptance rate if you wish so. But I see no issue with the output. – Xi'an May 01 '15 at 20:20
  • Thanks for your feedback @Xi'an. Can you please give me more details regarding the scale parameter. – aloha May 01 '15 at 20:23
  • As you just mentioned, if you increase your MCMC scale parameter, the acceptance rate drops to 30%-40%. You can experiment until you reach the 25% level, even though it should not make a difference in the outcome. – Xi'an May 01 '15 at 20:25
  • Exactly, it did not make a difference in the outcome. Thanks for your help @Xi'an. – aloha May 01 '15 at 20:54

1 Answers1

1

From the information you've given, there is no reason Not to trust your results. The best way, in this case, to double check if these results are reasonable is to plot a line using your best-fit parameters and see if it fits the data by eye. You can also look at the chi-squared value --- is that reasonable as-well?

If you're surprised that the walkers are converging to the result after only 10% of your steps, note that you chose the number of steps arbitrarily. The starting points, and shape of the likelihood distribution determine how quickly the walkers will converge.

DilithiumMatrix
  • 137
  • 7