0

I have temperature data of July 1991 to 2007, and wants to find the Confidence Interval at 95%, which distribution is best fit the data, Z or T. Please give me reason also.

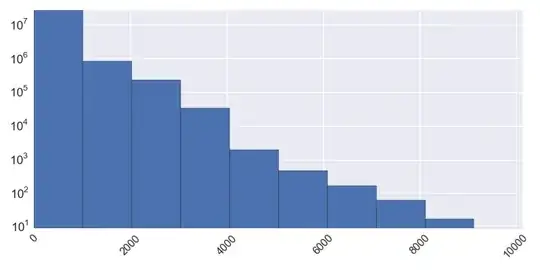
enter image description here

minTemp = 14.4444, maxTemp = 38.3333, SizeofData = 527, (17 years) hist(July, 20), histfit(July, 20);

Tim
  • 108,699
  • 20
  • 212
  • 390
Ahsan
  • 9
  • 5
  • 2
    Without knowing anything about your data it is impossible to answer your question. I imagine that there are areas in the world where temperature is pretty stable and areas where it varies depending on time of the year. – Tim Apr 27 '15 at 07:45
  • What type of information would be required to ans the question, i'll provide. – Ahsan Apr 27 '15 at 07:50
  • It would be good if you described your data in greater detail providing a data sample or plot as illustration etc. – Tim Apr 27 '15 at 07:51
  • 2
    Do you have any ideas why there is nothing above 38.3 degrees? Is it some kind of measurement error? – Tim Apr 27 '15 at 08:11
  • No it's not an error. – Ahsan Apr 27 '15 at 09:32
  • 1
    I ask because there is a pretty sharp drop. The data looks pretty normal but the drop - so the question is how the drop appeared? Is the data rather truncated or censored? If you want valid intervals those are the questions you have to ask yourself. – Tim Apr 27 '15 at 09:36
  • okay what will happen if i apply the Z-test, do i not get the correct interval at upper bound ? – Ahsan Apr 27 '15 at 09:53
  • Ahsan, are you sure you want a confidence interval (for what? the mean temperature?) or are you interested in the quantiles of the observed distribution? – A. Donda Apr 27 '15 at 13:36
  • I am interested in finding the confidence intervals, – Ahsan Apr 27 '15 at 17:56

1 Answers1

2

The first thing that could be noticed about your data is that there is a strange and sharp drop in the values below the 38.88 value. This looks like the data was truncated, i.e. "something" happen that the values above this value were not observed in your sample. If it was so, then using estimates from your data would give you biased (shifted to the left) estimates about the population. Consider the example below, where I generated some data with known $\mu$ and $\sigma^2$, from Normal distribution truncated at some point U, so that it resembles your data. Next I computed maximum likelihood estimate of truncated Normal distributions for $\mu$ and $\sigma^2$. As you can see, the ML estimates have better fit then the mean and sd estimated on the sample data.

set.seed(123)

U <- 37
x <- rnorm(500, 30, 5)
x <- x[x < U]

library(truncnorm)

llik <- function(param) -sum(log(dtruncnorm(x, mean=param[1], sd=param[2], b=U)))
optim(par=c(1, 1), llik, method = "L-BFGS-B", lower=c(1,1), upper=c(100, 100))

enter image description here

This however assumes that the distribution of your data is truncated. If it is not truncated and little is known about the distribution, then I would use bootstrap for constructing intervals as it does not have any distributional assumptions.

Community
  • 1
Tim
  • 108,699
  • 20
  • 212
  • 390
  • Although you provided the good example, but my data is not truncated, it's represent the 17th years of data of July, which means the data was not provided to me after 17th years. – Ahsan Apr 27 '15 at 18:00
  • Evidently you have daily data, which is why your sample size is given as 527 and (as the histogram shows even if that detail is not noticed) bin frequencies average about 30. I join @Tim in being worried on your behalf about the cut-off, which seems implausible for such temperature data. The highest temperature 38.3$^\circ$ C ($\approx$ 101$^\circ$ F for climatologically-challenged readers in the USA) is not so hot as to hint at measurement problems. Bottom line: worrying about confidence intervals is moot if the data can't be trusted. – Nick Cox Apr 27 '15 at 18:34