6

I've been trying to read the Wikipedia article on multivariate random variables but I'm having trouble getting past the math. Is there a more intuitive explanation?

I'm assuming that a univariate random variable is the same as a random variable, for example: the outcome of throwing a die. Is the outcome of throwing two dice simultaneously a multivariate variable?

nachocab
  • 505
  • 1
  • 4
  • 10
  • 4
    The concept is made obvious using the tickets-in-a-box model I have used to [explain univariate random variables](http://stats.stackexchange.com/a/54894/919), which includes an explanation of multivariate random variables (in the section immediately following the definition "a random variable is any consistent way to write numbers on tickets in a box"). In particular, the *outcome* of two dice is decidedly *not* a random variable, but writing down an ordered pair of numbers to represent that outcome is a multivariate RV. – whuber Apr 24 '15 at 20:09

2 Answers2

9

Yes, throwing two dice is a multivariate random variable. Specifically, you will get two independent and identically distributed discrete variables (assuming fair dice).

Throwing two dice and adding the results gets you a univariate random variable, with possible values between 2 and 12.

Picking a person at random and noting both their biological sex and their height is another multivariate random variable: a binary one and a more-or-less continuous one, and the two will not be independent any more.

One could argue that much of applied statistics is about drawing multivariate random variables and understanding just how exactly they are dependent. People will usually call all but one dimension "independent variables" and the last dimension "the dependent variable". You can also influence variables through your treatment.

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
  • 2
    Saying that "throwing two dice" is a multivariate RV falls short of answering the question. It's still vague. First, you have to stipulate how the outcome is expressed *numerically.* Second, you have to be clear that the two values are written down in a particular order. The second example, of observing two numerical attributes of a randomly chosen individual in a population, is a much better illustration. The second part about independent and dependent RVs gets off track again: the distinction is a distraction in this context. – whuber Apr 24 '15 at 20:13
3

With multivariate distributions, correlations between variables are important. If there is no correlation between to variable, then you basically have two univariate distributions.

Throwing two die would be a multivariate distribution, but would probably have a correlation of zero (the exceptions to this are interesting. For example, if you have two loaded dice from the same factor, the two die would probably be correlated!).

In morphometrics people study how different measurements of animals vary. For example, one might care that weight and height are correlated. You might also appreciate this article's other biology and genomic examples

If simulations help you to learn by exploring data, here's some code to help you get started exploring a multivariate normal distribution in R: library(MASS)

Sigma <- matrix(c(10, 4, 10, 4),2,2) 
d <- mvrnorm(n = 3000, mu = c(10, 3), Sigma = Sigma)
plot(d)

That produces this figure: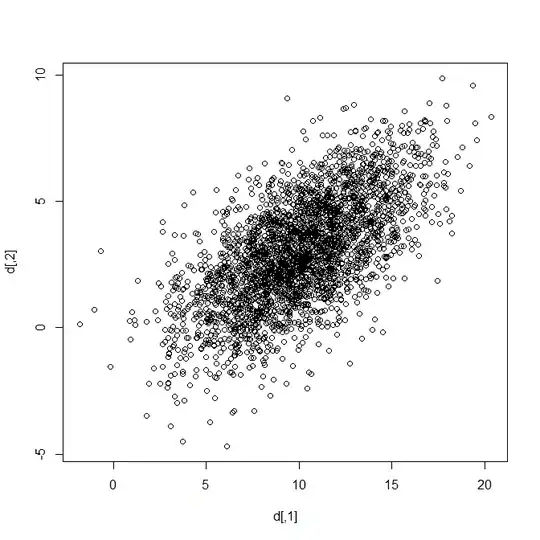enter image description here

Edit: I corrected my answer based upon the comment.

Richard Erickson
  • 466
  • 1
  • 6
  • 19
  • 4
    Two separate tosses of a loaded die will not be correlated. You might find it illuminating to work through the calculations and definitions to understand why not. – whuber Apr 24 '15 at 20:15
  • 1
    @whuber: Thank you. After thinking it through more, I see why you are correct. To make two die be (or at least appear to be) correlated, you need the thrower to be biased some how, correct? I am assuming the Vegas security people know how to look for this... – Richard Erickson Apr 24 '15 at 20:25
  • 2
    Correlation--or, strictly speaking, lack of independence--means that the results of one throw enable the results of the second throw to be more reliably predicted than if you did not know the outcome of the first throw. This concept has nothing to do with the actual chances of the outcomes. When someone throws two dice simultaneously, the concurrent conditions governing the physics of their rolls could indeed induce correlation, but when the dice are thrown separately and as randomly as possible, no correlation will exist. – whuber Apr 24 '15 at 20:28