Molecules movement distribution puzzle

Question

Let's say I have blood samples of whiteblood cells ($x$) and viruses ($v$). Space has been discretized in $LL$ spaces. They have a $p_v$ probability of interacting when found in the same space. I want to know at each sample how many $x$ and $v$ are interacting.

Here is a naive implementation of the model:

LL <- 1e4
nx <- 5000
nv <- 500
x <- c(rep(1,nx),rep(0, LL-nx))
v <- c(rep(1,nv),rep(0, LL-nv))
pv <- 0.8
t1 <- sapply(1:1e4, function(z) sum(sample(v)==1 & sample(x)==1 & runif(LL)<pv))

t1 represents how many times $x$ and $v$ interacted, in each of 1e4 samples.

I want to model this using a probability distribution, in order to make it more efficient. I think we can see this problem as a Binomial (and later maybe approximate with a Poisson), but I am not sure what arguments to pass to the Binomial. I can think of:

• at each space, there is a probability they are interacting, depending on their concentrations
• for each $x$, the probability is given by the concentration of $v$
• for each $v$, the probability is given by the concentration of $x$

In the first two cases, I have to limit the Binomial result to $nv$, which is the lowest value of molecules, and thus no more interactions than those are possible.

limit <- function(z)
    sapply(z, function(z) min(z,nx,nv))
t3 <- limit(rbinom(1e4, LL, pv*nx*nv/(LL*LL)))
t4 <- limit(rbinom(1e4, max(nx,nv), pv*min(nx,nv)/LL))
t5 <- rbinom(1e4, min(nx,nv), pv*max(nx,nv)/LL)

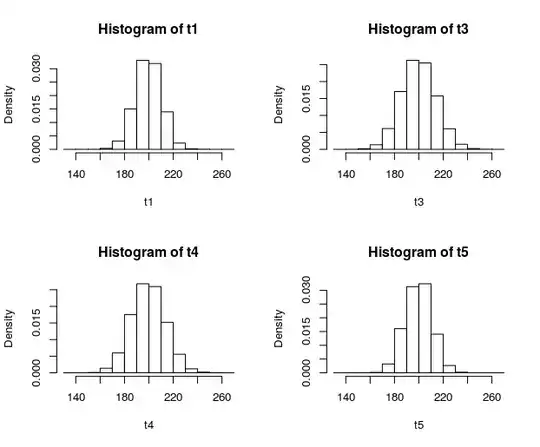
The histograms:

par(mfrow=c(2,3))
b <- seq(130, 270, 10)
hist(t1,b,FALSE)
hist(t3,b,FALSE)
hist(t4,b,FALSE)
hist(t5,b,FALSE)

print(sprintf("mean: %.3f x %.3f x %.3f x %.3f x %.3f",mean(t1),mean(t3),mean(t4),mean(t5)))
print(sprintf("sd: %.3f x %.3f x %.3f x %.3f x %.3f",sd(t1),sd(t3),sd(t4),sd(t5)))

Output:

[1] "mean: 200.036 x 200.281 x 199.991 x 200.108"
[1] "sd: 10.660 x 14.076 x 13.817 x 10.841"

The result suggests the latter maybe. Would love to have some feedback on this though. Thank you so much !

Answer 1

So, my question was whether the problem I presented could be modeled using a popular probability distribution.

The 3rd distribution I proposed seemed to work pretty well: $X\sim\mathcal{B}(\min(n_x,n_v),p_v\max(n_x,n_v)/LL)$. But it was still a little off. Besides, I was puzzled as to the differences between the distributions I proposed

@whuber (in a comment below) suggested this was so because I was constraining the distribution to $n_v$, but not to $n_x$; in other words, I was sampling $n_x$ independently of $LL$.

Taking that into account, this code seems like the correct distribution:

t6 <- sapply(1:nsim, function(z) {
    n <- 0
    for(vi in 1:nv)
        if(runif(1) < pv*(nx-n)/(LL-vi+1))
            n <- n+1
    n
})

Edit: Based on a 2nd suggestion by @whuber, I think we can use the hypergeometric distribution for this, $\mathcal{H}(nx,LL-nx,nv)$ ! (The idea being that I, and the other viruses, are choosing balls in a urn: they can either have a WTC there or not.)

t7 <- rhyper(nsim, nx, LL-nx, nv)

Comparing histograms:

Comparing means and standard deviations:

print(sprintf("mean: %.3f x %.3f x %.3f x %.3f x %.3f x %.3f",mean(t1),mean(t3),mean(t4),mean(t5),mean(t6),mean(t7)))
print(sprintf("sd: %.3f x %.3f x %.3f x %.3f x %.3f x %.3f",sd(t1),sd(t3),sd(t4),sd(t5),sd(t6),sd(t7)))
[1] "mean: 12.495 x 12.495 x 12.520 x 12.497 x 12.500 x 12.484"
[1] "sd: 2.178 x 3.303 x 3.064 x 2.496 x 2.174 x 2.182"