5

I have hourly temperature data over a 5 year period with a lot of missing values. They have 2 seasonal periods: daily (24) and annual (365*24). I am very interested in the diurnal cycles of the temperature. Is it possible to forecast (or "backcast") the missing values, which are mostly 2000 values straight? Here is one of my datasets: http://www.file-upload.net/download-10551392/BaiMu.txt.html

Because I wanted to do a decomposition of my data and since decompose or stl doesn't handle missing values, I extracted a period of my timeseries without missing values: Station <- 2

TMP <- which(!is.na(BaiMu[,2]))
Station <- BaiMu[min(TMP):max(TMP),c(1,Station)]
Station <- Station[23509:length(Station[,2]),]

Then I tried a simple forecast:

Station.ts <- ts(Station[,2], start=c(1,1+as.numeric(format(Station[1,1], "%H"))), 
frequency=24) 
require(forecast) 
plot(forecast(Station.ts, h=240))

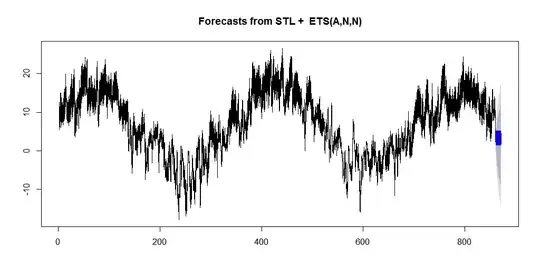
plot of the forecast

The forecast obviously didn't work. What did I do wrong?

Next I tried an auto.arima forecast:

Station.arima <- auto.arima(Station.ts)
plot(forecast.Arima(Station.arima, h=240))

That took a very long time and then also didn't work. Is there any way to forecast hourly time series up to 2000 values in R? How can I estimate the missing temperature values with R using the values before the gap and after it?

I also have temperature data from loggers nearby. Maybe I could estimate the 2 seasons and the trend of both time series (missing-value-logger (A) and non-missing-value-logger nearby (B)), then find out the random component of the B in the time period of the missing values of A and then add the seasonal components and trend of A to the random component of B. I tried decompose(), first with the daily season, and then removed the seasonal components:

Station.dec <- decompose(Station.ts)$figure
Station.seas <- rep(Station.dec, 1+length(Station.ts)/24)[1:length(Station.ts)]
plot(decompose(ts(Station.ts-Station.seas, start=c(1,1+as.numeric(format(Station[1,1], "%H"))), frequency=365*24)))

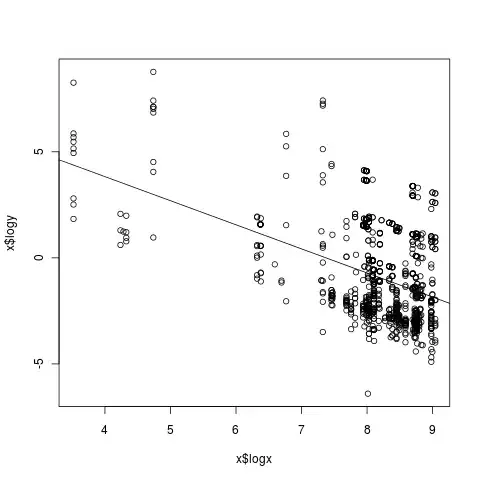plot of decomposition But the decomposition with decompose didn't show good results, because there was no random component (for A) but only season and trend. I think that's not possible because there always has to be a random component. Is that right? How I could use a sine and cosine equation to represent the seasons?

To summarize my questions: 1) Is it possible to forecast and/or backcast hourly time up to 2000 values? How could I do this?

2) How can I calculate and remove the seasonal components for an hourly time series with 2 seasons (daily and annual)? Is there any R function to do this?

I would be very thankful for any help, because I am relatively new to time series statistics.

yPennylane
  • 235
  • 2
  • 8
  • If you accept some simplifications (mainly that the seasonal cycles remain constant over the sample), you could define Fourier terms as proposed for example [here](http://robjhyndman.com/hyndsight/dailydata/) and include them in an ARIMA model. If you manage to fit the ARIMA model, you could fill the missing observations following the idea described in my answer to [this question](http://stats.stackexchange.com/questions/104565/). Differences of order 24 may be necessary, i.e., the model may be of the type ARIMA(p,24,q). Even though this is a simplified approach, it may be hard in practice. – javlacalle Apr 19 '15 at 23:47
  • Thank you for the advice. How do I actually identify the seasons? I think, I have a season with the period 24 which ist nested into a season with the period 24*365. Maybe there are more seasons, which I didn't discover yet. How do I find out, how many seasons are there and what period they could have? Also the "short" seasonality (period 24) is not constant over the year. The diurnal cycle of temperature varies from summer to winter. How can I decompose the time series and get the 2 seasons (period1=24, period2=24*365)? – yPennylane May 06 '15 at 18:57
  • 1
    1) You can look at the spectrum of the data to see which cycles are more relevant to explain the variability of the data. [This post](http://stats.stackexchange.com/questions/1207/period-detection-of-a-generic-time-series) may also help you. 2) You can try the function `tbats` in the `forecast` R package, which can deal with changing patterns in cycles and allows as input a time series with multiple seasonal periods (multiple periodicities that you may have detected using the ideas mentioned before). – javlacalle May 07 '15 at 08:50

0 Answers0